Bài toán thú vị nhỉ.
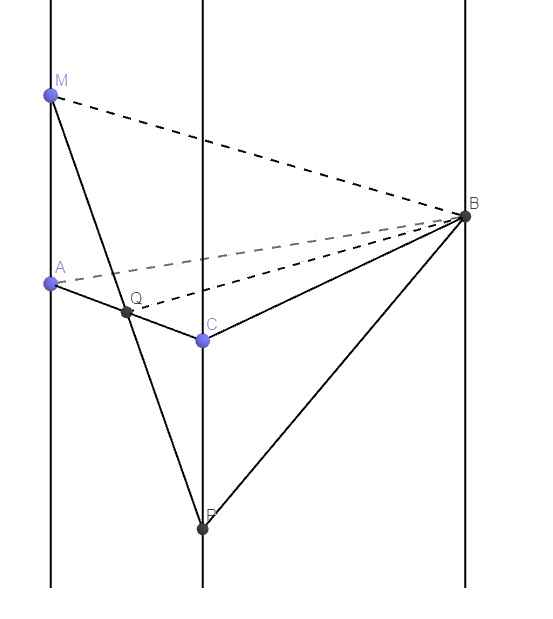
Do có vô số mp (P) thỏa mãn (là tất cả các mp song song với 1 mặt phẳng gốc) nên ta dựng mp (P) đặc biệt 1 chút để dễ tính toán và dựng hình (khỏi phải lấy nhiều điểm phụ): chọn vị trí (P) sao cho N trùng B
Gọi Q là trung điểm AC.
Do tam giác MBP đều \(\Rightarrow BM=BP\)
Mà \(AB=BC\Rightarrow\Delta_vABM=\Delta_vCBP\) (ch-gn)
\(\Rightarrow AM=CP\)
Nếu M và P nằm cùng phía so với mp (ABC) \(\Rightarrow ACPM\) là hcn \(\Rightarrow MP=AC\)
Mà MBP đều \(\Rightarrow AC=MP=BM>AB\) (cạnh huyền lớn hơn cạnh góc vuông) vô lý do AC=1 còn AB=2
Do đó M và P phải nằm khác phía so với mp (ABC)
AM và CP song song và bằng nhau nên AMCP là hình bình hành \(\Rightarrow\) Q đồng thời là trung điểm MP
\(\Rightarrow BQ\perp MP\) , mà \(BQ\perp AC\) \(\Rightarrow BQ\perp\left(AMCP\right)\)
Mà BQ là giao tuyến (ABC) và (P) \(\Rightarrow\widehat{MQA}=\alpha\)
\(BQ=\sqrt{AB^2-\left(\dfrac{AC}{2}\right)^2}=\dfrac{\sqrt{15}}{2}\)
Mà \(BQ=\dfrac{MP\sqrt{3}}{2}\Rightarrow MP=\sqrt{5}\) \(\Rightarrow MQ=\dfrac{1}{2}MP=\dfrac{\sqrt{5}}{2}\)
\(cos\alpha=\dfrac{AQ}{MQ}=\dfrac{1}{\sqrt{5}}\Rightarrow\alpha\)