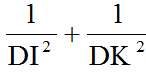Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Các câu hỏi tương tự
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ đường thẳng cắt BC ở E và cắt đường thẳng DC ở F. Chứng minh: \(\dfrac{1}{AE^{2^{ }}}+\dfrac{1}{ÀF^2}=\dfrac{1}{a^2}\)
help me
cho tam giác ABC vuông tại A có đường cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB,AC. cho BH= 3cm, CH= 12cm
a, tính độ dài các cạnh AB,AC
b, chứng minh HF= 2HE
c, từ C kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AB tại I, kẻ AK vuông góc với CI tại K. chứng minh
CI^3/CB^3= IK/BH
CHo tam giác ABC vuông tại A, đường cao AH, đường phân giác AD chia cạnh đối diện BC thành hai đoạn thẳng BD=36cm, CD=60cm.Tìm tỉ số \(\dfrac{HB}{HC}\)và tính AH
cho tam giác ABC vuông tại A, đường cao AH . Cho biết BH =4, CH=9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạnh AB, AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M,N. Tính diện tích tứ giác DENM
MÌNH ĐANG CẦN GẤP MN GIÚP MIK VS Ạ ! MIK CẢM ƠN !
giúp mk bài này vs Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:a) Tam giác DIL là một tam giác cânb) Tổngkhông đổi khi I thay đổi trên cạnh AB.
Đọc tiếp
giúp mk bài này vs
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng
không đổi khi I thay đổi trên cạnh AB.
cho hình vuông ABC , E à điểm năm giữa A và B . Tia DEvà tia CB cắt nhau ở K. kẻ qua D 1 đường thẳng vuống góc với DE cắt đường thẳng BC tại H
CMR: 1) tam giác DEH cân
2) 1 phần DE mũ 2 cộng 1 phần DK mũ 2 không đổi khi E thay đổi trên cạnh AB
cho hình chữ nhật ABCD, AB=36, AD=24. E là trung điểm của AB, đường thẳng DE cắt AC tại F, cắt BC tại G.
a) CMR: \(FD^2=FE.FG\)
b) tính DG
cho hcn abcd (ab<ad). Qua a vẽ đường thẳng vuông góc với bd, đường thẳng này cắt bd,cd,bc lần lượt tại h,e,f
1/cm tg fhb đồng dạng tg dhe
2/ cm hd.hb=he.hf
Cho hình chữ nhật ABCD (AB lớn hơn AC) . Kẻ AH vuông góc BD tại H . AH cắt DC tại K và cắt đường thẳng BC tại M A) Chứng minh DH.DB=AH.AK và BC.BD=AH.AM B) Chứng minh AD bình = DK.DC C) Chứng minh AH bình= HK.HM