Question

Cho hình 72, trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng 3 điểm A, O, C thẳng hàng

Answer 1

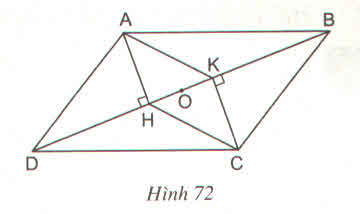
a) Hai tam giác vuông AHD và CKD có:

AD = CB (gt)

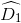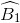= (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.

Answer 2

Tham khảo thôi!

a) Hai tam giác vuông AHD và CKD có:

AD = CB (gt)

\(\widehat{D_1}\) = \(\widehat{B_1}\) (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.