Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Các câu hỏi tương tự
6 tháng 2 2022 lúc 15:49
Cho hàm số \(f\left(x\right)=\dfrac{x-m^2}{x+8}\)với m là tham số cực . Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn \(\left[0;3\right]=2\)
Có bao nhiêu giá trị thực của tham số m để hàm số y = \(\left|x^2+mx+1\right|\) trên [-1;2] đạt giá trị nhỏ nhất bằng 1
cho hàm số y=\(\dfrac{x^2-m^2x+1}{x-1}\).Gọi S là tập hợp tất cả giá trị thực của tham số m để max=14/3
Tìm tất cả các giá trị m để giá trị nhỏ nhất của hàm số:1/ ydfrac{x+m}{x-1} trên left[2;4right] bằng 3.2/ y2x^3-3x^2-m trên left[-1;1right] bằng 1.3/ yleft|x^3-3x^2+mright| trên left[0;3right] bằng 2.
Đọc tiếp
Tìm tất cả các giá trị \(m\) để giá trị nhỏ nhất của hàm số:
1/ \(y=\dfrac{x+m}{x-1}\) trên \(\left[2;4\right]\) bằng 3.
2/ \(y=2x^3-3x^2-m\) trên \(\left[-1;1\right]\) bằng 1.
3/ \(y=\left|x^3-3x^2+m\right|\) trên \(\left[0;3\right]\) bằng 2.
Tìm tất cả giá trị m để giá trị lớn nhất của hàm số:1/ ydfrac{2x+m}{x+1} trên left[0;1right] bằng 2.2/ yleft|x^3-3x^2+mright| trên left[0;3right] bằng 5.3/ yleft|dfrac{x^2+mx+m}{x+1}right| trên left[1;2right] bằng 2.4/ yleft|dfrac{1}{4}x^4-dfrac{19}{2}x^2+30x+m-20right| trên left[0;2right] không vượt quá 20.
Đọc tiếp
Tìm tất cả giá trị \(m\) để giá trị lớn nhất của hàm số:
1/ \(y=\dfrac{2x+m}{x+1}\) trên \(\left[0;1\right]\) bằng 2.
2/ \(y=\left|x^3-3x^2+m\right|\) trên \(\left[0;3\right]\) bằng 5.
3/ \(y=\left|\dfrac{x^2+mx+m}{x+1}\right|\) trên \(\left[1;2\right]\) bằng 2.
4/ \(y=\left|\dfrac{1}{4}x^4-\dfrac{19}{2}x^2+30x+m-20\right|\) trên \(\left[0;2\right]\) không vượt quá 20.
Tìm tất cả các giá trị của m>1 để giá trị lớn nhất của hàm số f(x)=(2.cănx +m)/(căn(x+1)) trên đoạn [0,4] không lớn hơn 3
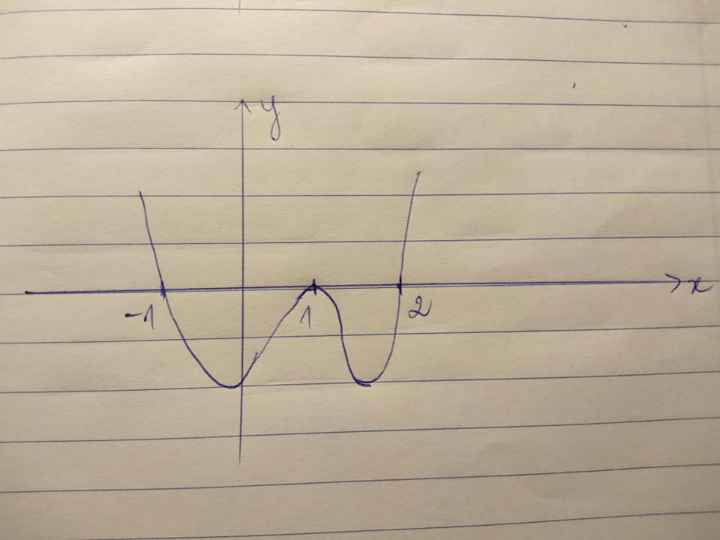
Cho hàm số y=f(x) liên tục trên R có đồ thị y=f '(x) như hình vẽ:
a)Tìm min, max của hàm số g(x)=f(\(\sqrt{8-x^2-2x}-1\))
b)Xác định khoảng đb, nb, cực đại, cực tiểu của g(x)=f(x2+x)
Có bao nhiêu giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm f(x)= \(\left|-x^3+2x^2-2x+m+2\right|\) trên đoạn [0;2] không vượt quá 10?
A.25 B.17 C.26 D.18
14 tháng 3 2021 lúc 21:26
Cho hàm số f(x) = \(\dfrac{x+m}{x+1}\) (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của tham số m sao cho \(max_{[0;1]}\left|f\left(x\right)\right|\) + \(min_{[0;1]}\left|f\left(x\right)\right|\) =2. Số phần tử của S là?