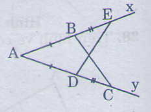
Ta có: AC=AD+DC
Hay AC= BA+BE
(do AD=AB, DE=BE)
Nên AC=AE.
∆ABC và ∆ ADE có:
AC=AE(chứng minh trên)
\(\widehat{A}\) chung
AB=AD(gt)
Vậy ∆ABC =∆ADE(c.g.c)
Bài 2. Cho góc xAy. Lấy điểm B trên Ax, điểm D trên Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh AABC = AADE
Bài 3. Cho góc nhọn xOy và tia Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm I thuộc tia Oz Chứng minh rằng a) AAOI = ABOI b) AB 1 OI
Bài 4. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC a) Chứng minh ABAC = ABAD b) Trên tia đối của tia AB lấy điểm M. Chứng minh AMBD = AMBC
cho góc xAy. Lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB=AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE=DC. Chứng minh rằng tam giác ABC=tam giác ADE
Cho góc xAy. Lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB= AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE= DC.
Chứng minh rằng tam giác ABC= tam giác ADE
Gọi O là giao điểm của BC và DE.
Chứng minh: AO là tia phân giác của tam giác BAD
#Giúp mình nha!!
cho tam giác ABC Có Góc A > 90 độ. Về phía trong của tam giác vẽ Ax vuông góc với AB. Trên Ax lấy điểm D sao cho AD=AB. Kẻ Ay sao cho Ay vuông góc với AC, Trên Ay lấy điểm E sao cho AE=AC. M là trung điểm của DE. Trên tia đối của tia MA lấy F sao cho MF=MA
a, Chứng minh:góc yAB = góc xAC
b, Chứng minh: EF vuông góc với AB
c, Chứng minh:tam giác ABC=tam giác ABF
cho tam giác ABC Có Góc A > 90 độ. Về phía trong của tam giác vẽ Ax vuông góc với AB. Trên Ax lấy điểm D sao cho AD=AB. Kẻ Ay sao cho Ay vuông góc với AC, Trên Ay lấy điểm E sao cho AE=AC. M là trung điểm của DE. Trên tia đối của tia MA lấy F sao cho MF=MA
a, Chứng minh:góc yAB = góc xAC
b, Chứng minh: EF vuông góc với AB
c, Chứng minh:tam giác ABC=tam giác ABF
Cho góc nhọn xoy .trên tia đối của tia ox lấy điểm a,trên tia đối của tia oy lấy điểm b sao cho oa=ob.trên tia ax lấy điểm c,trên tia by lấy điểm d sao cho ac=bd và ob<od,oa<oc
a) Chứng minh ad=bc
b) gọi e là giao điểm của advà bc.chứng minh tam giác eac= tam giác ebd
Bài 3 : Cho tam giác ABC , gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh : A là trung điểm của MN.
