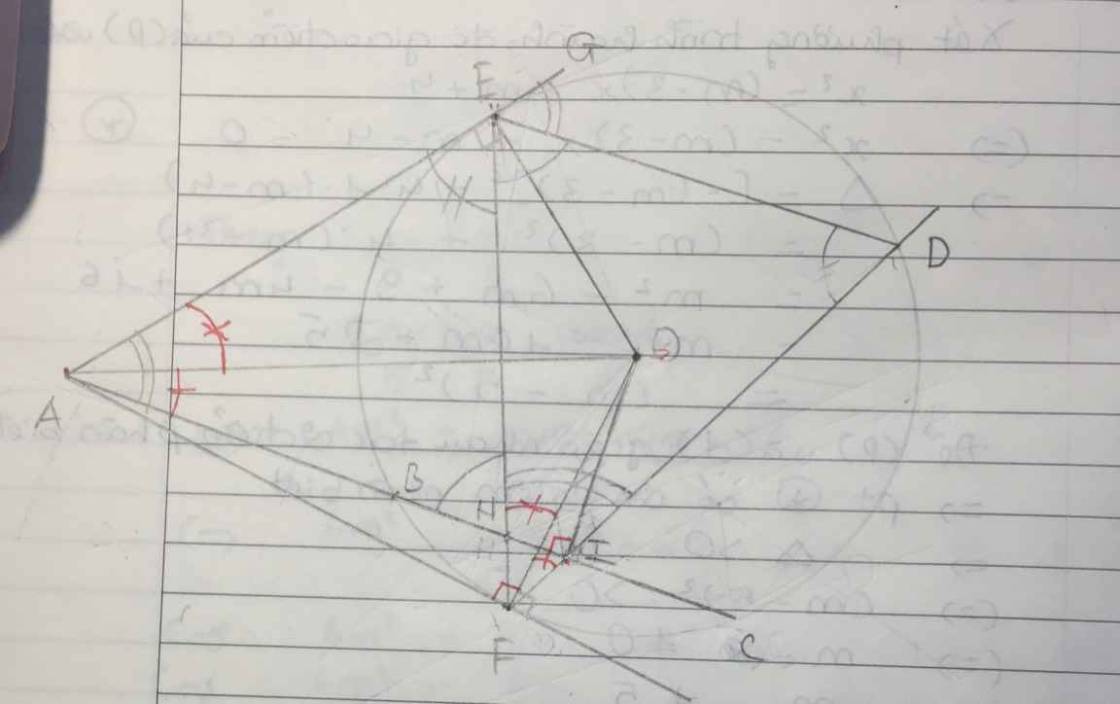
+ Cho đường tròn (O;R) và dây BC cố định. Trên tia đối của tia BC lấy điểm A. Kẻ các tiếp tuyến AM, AN với đường trong (O) (M và N là các tiếp điểm, N thuộc cung BC nhỏ). Gọi H là trung điểm của dây BC. a) Chứng minh: Tứ giác AMON và tứ giác AOHN nội tiếp. b) Chứng minh AB.AC = AM2. c) Tia MH cắt đường tròn (O) tại điểm thứ hai D. Giả sử ba điểm A, B, C cố định, đường tròn (O) di động. Chứng minh: ND // AC và đường thẳng MN luôn đi qua một điểm cố định.
a: ΔOBC cân tại O
mà OH là trung tuyến
nên OH vuông góc BC
góc OHA+góc ONA=180 độ
=>OHAN nội tiếp
góc OMA+góc ONA=90+90=180 độ
=>OMAN nội tiếp
b: Xét ΔAMB và ΔACM có
góc AMB=góc ACM
góc BAM chung
=>ΔAMB đồng dạng với ΔACM
=>AM/AC=AB/AM
=>AM^2=AB*AC
bài đầy đủ đây bạn nhé
https://www.youtube.com/watch?v=DiI4Jz-LYQ4