\(S_{OKN}=\dfrac{1}{2}\cdot OK\cdot KN< =\dfrac{1}{2}\cdot\dfrac{OK^2+ON^2}{2}=\dfrac{R^2}{4}\)
Dấu = xảy ra khi MO=MA
Đúng 0
Bình luận (1)
Ôn thi vào 10
Các câu hỏi tương tự
+ Cho đường tròn (O;R) và dây BC cố định. Trên tia đối của tia BC lấy điểm A. Kẻ các tiếp tuyến AM, AN với đường trong (O) (M và N là các tiếp điểm, N thuộc cung BC nhỏ). Gọi H là trung điểm của dây BC. a) Chứng minh: Tứ giác AMON và tứ giác AOHN nội tiếp. b) Chứng minh AB.AC AM2. c) Tia MH cắt đường tròn (O) tại điểm thứ hai D. Giả sử ba điểm A, B, C cố định, đường tròn (O) di động. Chứng minh: ND // AC và đường thẳng MN luôn đi qua một điểm cố định.
Đọc tiếp
+ Cho đường tròn (O;R) và dây BC cố định. Trên tia đối của tia BC lấy điểm A. Kẻ các tiếp tuyến AM, AN với đường trong (O) (M và N là các tiếp điểm, N thuộc cung BC nhỏ). Gọi H là trung điểm của dây BC. a) Chứng minh: Tứ giác AMON và tứ giác AOHN nội tiếp. b) Chứng minh AB.AC = AM2. c) Tia MH cắt đường tròn (O) tại điểm thứ hai D. Giả sử ba điểm A, B, C cố định, đường tròn (O) di động. Chứng minh: ND // AC và đường thẳng MN luôn đi qua một điểm cố định.
Cho đường tròn (O;R) và dây BC cố định không qua 0. Trên tia đối của tia BC lấy điểm A khác B. Tủ A kẻ các tiếp tuyến AM, AN với đường tròn (M, N là tiếp điểm). 1) Chứng minh bốn điểm A, M, O, N cũng thuộc một đường tròn. 2) MN cắt OA tại H. Chứng minh OAI MN và AH.AO = AB.AC.
cho đường tròn (o,r) có dây B,C ko đi qua tâm. từ điểm A thuộc tia đối của tia BC, vẽ các tiếp tuyến AE, AF của đường tròn O với E,F là các tiếp điểm. gọi I là trung điểm của BC, D là giao điểm thứ 2 của FI và (O), H là giao điểm của EF và AC. chứng minh: a) ED//ACb) AH.AI AB.ACgiúp mình câu b thôi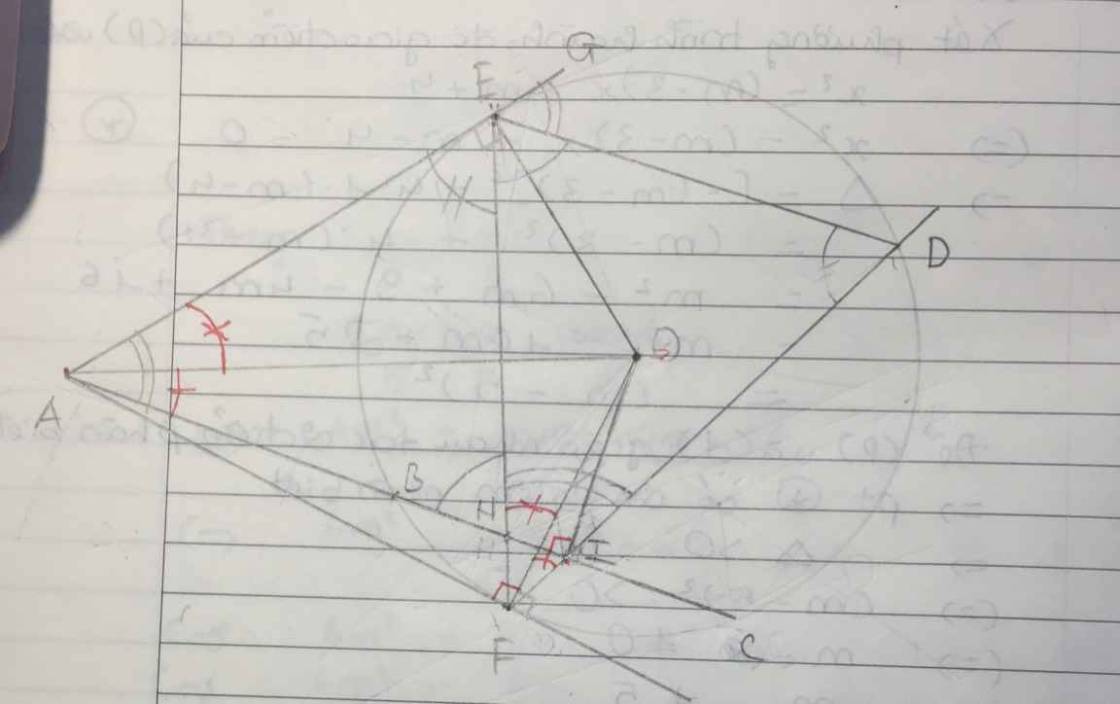
Đọc tiếp
cho đường tròn (o,r) có dây B,C ko đi qua tâm. từ điểm A thuộc tia đối của tia BC, vẽ các tiếp tuyến AE, AF của đường tròn O với E,F là các tiếp điểm. gọi I là trung điểm của BC, D là giao điểm thứ 2 của FI và (O), H là giao điểm của EF và AC. chứng minh:
a) ED//AC
b) AH.AI = AB.AC
giúp mình câu b thôi 
17 tháng 5 2022 lúc 8:19
Cho điểm M nằm ngoài đường tròn (O;R). Vẽ tiếp tuyến MA (A là tiếp điểm), cát tuyến MBC (B nằm giữa M và C) và O nằm trong góc AMC. Gọi I là trung điểm của BC. Tia OI cắt cung nhỏ BC tại N, AN cắt BC tại D
a) Cm AD là phân giác của góc BAC
b) Cm MD2 = MB. MC
c) Gọi H, K là hình chiếu của N lên AB và AC. Chứng minh ba điểm H,I,K thẳng hàng
Cho đường tròn (O;R) với dây CD cố định .Điểm M thuộc tia đối của tia DC.Qua M kẻ hai tiếp tuyến MA,MB tới đường tròn (O;R) (A thuộc cung lớn CD) . Gọi I là trung điểm của CD , OM cắt AB tại H.Tia OI cắt AB tại K ,nối AB cắt CD tại Ea) C/m 4 điểm M,H,I,K cùng thuộc 1 đường trònb) C/m ME.MIMA^2c) Xác định vị trí của M để tam giác MAB đềud) C/m KC là tiếp tuyến của đường tròn
Đọc tiếp
Cho đường tròn (O;R) với dây CD cố định .Điểm M thuộc tia đối của tia DC.Qua M kẻ hai tiếp tuyến MA,MB tới đường tròn (O;R) (A thuộc cung lớn CD) . Gọi I là trung điểm của CD , OM cắt AB tại H.Tia OI cắt AB tại K ,nối AB cắt CD tại E
a) C/m 4 điểm M,H,I,K cùng thuộc 1 đường tròn
b) C/m ME.MI=MA^2
c) Xác định vị trí của M để tam giác MAB đều
d) C/m KC là tiếp tuyến của đường tròn
Từ điểm A cố định nằm ngoài đường tròn (O;R), dựng các tiếp tuyến AB, AC và cát tuyến ADE với đường tròn (B,C thuộc (O), D nằm giữa A và E). Gọi I là trung điểm của DE, H là giao điểm của AO và BC.
Qua I kẻ đường thẳng song song với BE, cắt BC tại M. Chứng minh rằng DM vuông góc với BO
Cho đường tròn (O; R) và dây MN không đi qua tâm O. Kẻ đường kính AB vuông góc với MN tại E. Lấy điểm C thuộc dây MN. BC cắt đường tròn (O;R) tại K. a) Chứng minh: Tứ giác AKCE nội tiếp b) Gọi I là giao điểm của AK và MN, D là giao điểm của AC và BI. Chứng minh C cách đều 3 cạnh của tam giác DEK
Từ điểm A ở ngoài đường tròn tâm O, vẽ 2 tiếp tuyến AB và AC với (O) (B và C là các tiếp điểm). OA cắt BC tại H, cắt đường tròn (O) tại 2 điểm I và K (I thuộc cung BC nhỏ, K thuộc cung BC lớn). Vẽ đường kính CD, cát tuyến AD cắt (O) tại M. BM cắt OA tại NChứng minh: a) Tứ giác AMHC nội tiếp b) N là trung điểm của AH c) 1/AN1/AI+1/AK
Đọc tiếp
Từ điểm A ở ngoài đường tròn tâm O, vẽ 2 tiếp tuyến AB và AC với (O) (B và C là các tiếp điểm). OA cắt BC tại H, cắt đường tròn (O) tại 2 điểm I và K (I thuộc cung BC nhỏ, K thuộc cung BC lớn). Vẽ đường kính CD, cát tuyến AD cắt (O) tại M. BM cắt OA tại N
Chứng minh: a) Tứ giác AMHC nội tiếp
b) N là trung điểm của AH
c) 1/AN=1/AI+1/AK
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R);(AB>AC).Gọi M là điểm chính giữa cung BC; OM cắt BC tại D; AM cắt BC tại K a)chứng minh AM là tia phân giác của BAC b)Tiếp tuyến tại A của đường tròn tâm O cắt BC tại S.Chứng minh SA²=SB.SC c)chứng minh SA=SK và S;A;O;D cùng thuộc 1 đường tròn d)Trên đường tròn tâm O đặt E sao cho SB.SC=SE² chứng minh điểm E nằm trên đường tròn (SAOD)