Question

Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không cần dùng thước đo.

Answer 1

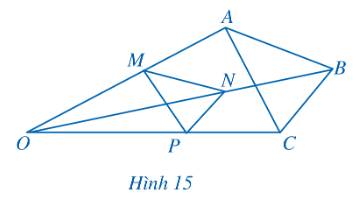
Lấy một điểm P nằm ngoài đoạn thẳng AB và nối AP, BP.

Trên đoạn thẳng AP lấy hai điểm M và N sao cho AM = MN = NP.

Khi đó \(\frac{{AM}}{{AP}} = \frac{1}{3};\,\,\frac{{AN}}{{AP}} = \frac{2}{3}\).

Kẻ các đoạn thẳng \(MC\parallel PB,\,\,ND\parallel PB\) với \(C,\,\,D \in AB\).

Theo hệ quả của định lý Thales trong tam giác APB thì \(\frac{{AM}}{{AP}} = \frac{{AC}}{{AB}} = \frac{1}{3}\) và \(\frac{{AN}}{{AP}} = \frac{{AD}}{{AB}} = \frac{2}{3}\).

Khi đó AC = CD = DB = \(\frac{1}{3}\)AB.

Vậy ta đã chia đoạn thẳng AB thành 3 phần bằng nhau mà không cần dùng thước đo.