Cho hai đoạn thẳng AB = 2cm, CD = 3cm và hai đoạn thẳng MN = 4cm, PQ = 6cm. So sánh hai tỉ số \(\frac{{AB}}{{CD}},\,\,\frac{{MN}}{{PQ}}\).
Bài 1. Định lí Thalès trong tam giác
Hoạt động 1 (SGK Cánh Diều trang 52)
Thảo luận (1)
Hoạt động 2 (SGK Cánh Diều trang 53)
Quan sát Hình 3 và cho biết:
a) Đường thẳng \(d\) có song song với BC hay không?
b) Bằng cách đếm số ô vuông, dự đoán xem các tỉ số \(\frac{{AM}}{{MB}},\frac{{AN}}{{NC}}\) có bằng nhau hay không?
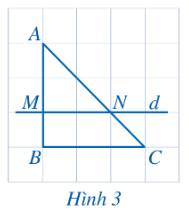
Thảo luận (1)Hướng dẫn giảia) Quan sát hình ta thấy \(d\parallel BC\).
b) Ta thấy:
Độ dài AM là 2 lần cạnh của một ô vuông.
Độ dài MB là cạnh của một ô vuông.
\( \Rightarrow \frac{{AM}}{{MB}} = \frac{2}{1} = 2\)
Độ dài AN là 2 lần đường chéo của một ô vuông.
Độ dài NC là độ dài đường chéo của một ô vuông.
\( \Rightarrow \frac{{AN}}{{NC}} = \frac{2}{1} = 2\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
(Trả lời bởi Hà Quang Minh)
Luyện tập 1 (SGK Cánh Diều trang 53)
Trong Hình 4, chứng tỏ rằng nếu \(MN\parallel BC\) thì \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\).
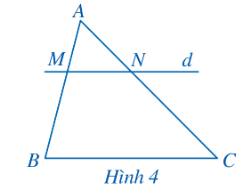
Thảo luận (1)Hướng dẫn giảiXét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).
(Trả lời bởi Hà Quang Minh)
Luyện tập 2 (SGK Cánh Diều trang 53)
Cho tam giác ABC có M là trung điểm của cạnh AB. Đường thẳng qua M song song với BC cắt cạnh AC tại N. Chứng minh N là trung điểm của cạnh AC.
Thảo luận (1)Hướng dẫn giảiGọi AD là đường trung tuyến của tam giác ABC (D \(\in\) BC)
Vì G là trọng tâm của tam giác ABC nên AG = \(\frac{2}{3}\) AD hay \(\frac{AG}{AD} =\frac{2}{3}\) .
Xét tam giác ABD với MG // BD, ta có:
\( \frac {AM}{AB} = \frac{AG}{AD} =\frac{2}{3}\) (Định lí Thales) (1)
Tương tự, xét
tam giác ADC với GN // DC, ta có:
\( \frac {AN}{AC} = \frac{AG}{AD} =\frac{2}{3}\) (Định lí Thales) (2)
Từ (1) và (2) suy ra \( \frac{AM}{AB} = \frac{AN}{AC} = \frac{2}{3} \) (đpcm).
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (SGK Cánh Diều trang 53)
Trong Hình 7, cho AM = 1, MB = 2, AN = 1,5, NC = 3.
a) So sánh các tỉ số \(\frac{{AM}}{{MB}};\,\,\frac{{AN}}{{NC}}\).
b) Đường thẳng \(d\) (đi qua M, N) có song song với BC hay không?
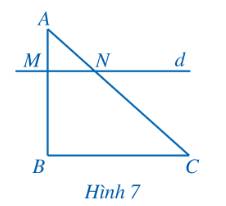
Thảo luận (1)Hướng dẫn giảia) \(\frac{{AM}}{{MB}} = \frac{1}{2}\)
\(\frac{{AN}}{{AC}} = \frac{{1,5}}{3} = \frac{1}{2}\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.
Xét ∆ABC’ với MN // BC’, ta có:
\( \frac{AM}{MB}=\frac{AN}{NC′}\) (định lí Thalès).
Mà theo câu a, \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) nên ta có \(\frac{{AN}}{{NC}} = \frac{AN}{NC′}\)
Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.
Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.
Vậy đường thẳng d (đi qua M, N) song song với BC.
(Trả lời bởi Hà Quang Minh)
Luyện tập 3 (SGK Cánh Diều trang 53)
Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.
Thảo luận (1)Hướng dẫn giảiXét tam giác ABC có
\(\begin{array}{l}\frac{{CM}}{{CA}} = \frac{1}{4}\\\frac{{CN}}{{CB}} = \frac{{1,25}}{5} = \frac{1}{4}\\ \Rightarrow \frac{{CM}}{{CA}} = \frac{{CN}}{{CB}}\end{array}\)
\( \Rightarrow MN\parallel AB\) (Định lý Thales đảo)
Mà \(AB \bot AC\) nên \(MN \bot AC\) hay tam giác MNC vuông tại M
Xét tam giác MNC vuông tại M có: \(MC = 1,\,\,NC = 1,25\).
Theo định lý Pytago ta có:
\(\begin{array}{l}M{N^2} + M{C^2} = N{C^2}\\\,\,\,\,\,\,\,M{N^2} + {1^2} = 1,{25^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 1,{25^2} - {1^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 0,5625\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,MN = 0,75\end{array}\)
Vậy MN = 0,75.
(Trả lời bởi Hà Quang Minh)
Bài 1 (SGK Cánh Diều trang 57)
Cho tam giác ABC có \(AB = 4,5cm,\,\,AC = 6cm\). Các điểm M, N lần lượt thuộc các cạnh AB, AC thỏa mãn \(AM = 3cm\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng AN.
Thảo luận (1)Hướng dẫn giảiXét tam giác ABC có \(MN\parallel BC\) nên:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (Hệ quả của định lý Thales)
\( \Rightarrow \frac{3}{{4,5}} = \frac{{AN}}{6} \Rightarrow AN = 6.3:4,5 = 4cm\).
(Trả lời bởi Hà Quang Minh)
Bài 2 (SGK Cánh Diều trang 57)
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
Thảo luận (1)Hướng dẫn giảia) Vì \(d\parallel CD\) nên \(MP\parallel CD\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{MD}} = \frac{{AP}}{{PC}}\,\,\left( 1 \right)\) (Định lý Thales)
Vì \(d\parallel AB\) nên \(PN\parallel AB\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{BN}}{{NC}} = \frac{{AP}}{{PC}}\,\,\left( 2 \right)\) (Định lý Thales)
Từ (1) và (2) ta có \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\).
b) Vì \(MD = 2MA\) nên \(\frac{{AM}}{{MD}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AD}} = \frac{1}{3}\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{AD}} = \frac{{MP}}{{DC}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{MP}}{{DC}} = \frac{1}{3} \Rightarrow MP = \frac{1}{3}DC = 2cm\)
Vì \(\frac{{AM}}{{AD}} = \frac{1}{3} \Rightarrow \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{CA}} = \frac{2}{3}\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{CP}}{{CA}} = \frac{{PN}}{{AB}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{PN}}{{AB}} = \frac{2}{3} \Rightarrow PN = \frac{2}{3}AB = \frac{8}{3}cm\)
Mà \(MN = MP + PM = 2 + \frac{8}{3} = \frac{{14}}{3}cm\).
(Trả lời bởi Hà Quang Minh)
Bài 3 (SGK Cánh Diều trang 57)
Trong Hình 15, cho \(MN\parallel AB,\,\,NP\parallel BC\). Chứng minh \(MP\parallel AC\).
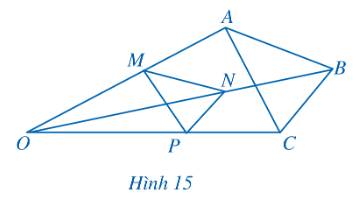
Thảo luận (1)Hướng dẫn giảiXét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Hệ quả của định lý Thales).
(Trả lời bởi Hà Quang Minh)
Bài 4 (SGK Cánh Diều trang 57)
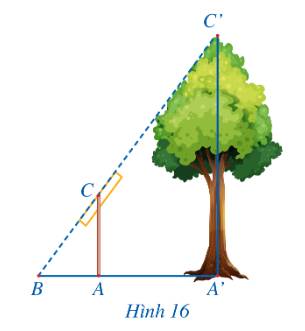
Trong Hình 16, độ dài đoạn thẳng A’C’ mô tả chiều cao của một cái cây, đoạn thẳng AC mô tả một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm A’, A, B). Giả sử \(AC = 2m,\,\,AB = 1,5m,\,\,A'B = 4,5m\). Tính chiều cao của cây.
Thảo luận (1)Hướng dẫn giải\(\left. \begin{array}{l}AC \bot A'B\\A'C' \bot A'B\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Xét tam giác A’BC’ với \(AC\parallel A'C'\) có:
\(\frac{{AC}}{{A'C'}} = \frac{{BA}}{{BA'}}\) (Hệ quả của định lý Thales)
\( \Rightarrow \frac{{AC}}{{A'C'}} = \frac{{1,5}}{{4,5}} = \frac{1}{3} \Rightarrow A'C' = 3AC = 6m\)
Vậy cây cao 6m.
(Trả lời bởi Hà Quang Minh)