Ta có: = mà CD= 12cm nên
= => A= = 9
Vậy độ dài AB= 9cm.
Vì \(\frac{AB}{CD}\) = \(\frac{3}{4}\) nên 4.AB = 3.CD mà CD = 12 cm \(\Rightarrow\) AB =\(\frac{3}{4}\).CD \(\Leftrightarrow\) AB = \(\frac{3}{4}\).12 = 9(cm).
Vậy AB = 9 cm
Ta có: = mà CD= 12cm nên
= => A= = 9
Vậy độ dài AB= 9cm.
Vì \(\frac{AB}{CD}\) = \(\frac{3}{4}\) nên 4.AB = 3.CD mà CD = 12 cm \(\Rightarrow\) AB =\(\frac{3}{4}\).CD \(\Leftrightarrow\) AB = \(\frac{3}{4}\).12 = 9(cm).
Vậy AB = 9 cm
Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A'B' gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A'B' ?
1) cho MN=2cm , PQ =5cm. tính tỉ số của 2 đoạn thẳng MN và PQ là:
2) Nếu AB=5m, CD =4dm thì:
3) cho biết \(\frac{AB}{CD}=\frac{3}{4}\)và \(CD=12cm\) thì độ dài của AB là:|
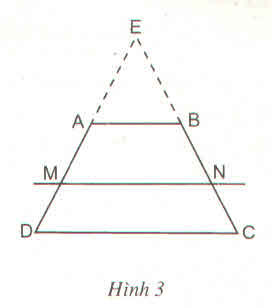
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Cho đoạn AB.C thuộc AB, D thuộc tia đối của tia BA sao cho \(\dfrac{CA}{CB}=\dfrac{DA}{DB}=2\). Biết CD=4cm, AB dài bao nhiêu cm
Cho hình thang ABCD có AB=3cm, CD=5cm (AB//CD). Lấy M,N thuộc AD, BC sao cho MN//AB và \(\dfrac{MA}{MD}=3\). Gọi I là giao điểm của AC và MN.
a) Tính tỉ số \(\dfrac{IA}{IC};\dfrac{NB}{NC}\)
b) Tính MN
Cho hình thang ABCD, AB // BC. I là giao của hai đường chéo. Qua I vẽ đường thẳng song song với hai đáy cắt AD tại E , BC tại F.
a, Chứng minh IE = IF
b, Chung minh \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{IE}\)
c, Chứng minh \(\dfrac{2}{EF}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
1.Cho 2 đoạn thẳng AB và CD tỉ lệ với 3 và 4 biết CD=15cm. Tính độ dài AB
2.Nếu ta có AB/CD=3/5 =>AB=3 ; CD=5. Đúng hay sai
2) Cho hình thang ABCD (AB//CD) giao điểm hai đường chéo là O. Đường thẳng O//AB cắt AD và BC lần lượt tại M,N.
a) C/m \(\dfrac{MO}{CD}+\dfrac{MO}{AB}=1\)
b) C/m \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\)
c) Biết \(S_{AOB}=m^2,S_{COD}=n^2\).Tính \(S_{ABCD}\) theo m và n (với \(S_{AOB},S_{COD},S_{ABCD}\)lần lượt là diện tích tam giác AOB, diện tích tam giác COD, diện tích tam giác ABCD)