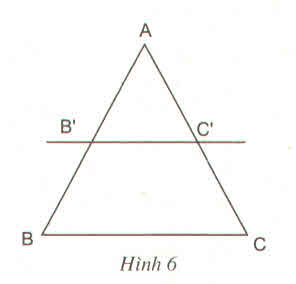
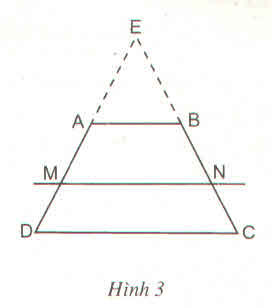
a) Ta có:
= => =
=> - 1 = =
=> = => =
b) Vì = mà AB' = AB - B'B, AC' = AC - C'C.
a) Ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\Rightarrow\dfrac{AB}{AC}=\dfrac{AB'}{AC'}\)
Áp dụng tc dãy tỉ số bằng nhau ta có;
\(\dfrac{AB}{AC}=\dfrac{AB'}{AC'}=\dfrac{AB-AB'}{AC-AC'}=\dfrac{BB'}{CC'}\)
\(\Rightarrow\dfrac{AB'}{AC'}=\dfrac{BB'}{CC'}\Leftrightarrow\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)
b) Ta có:
\(\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\left(cmt\right)\)
\(\Leftrightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Leftrightarrow\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)