Bài 1: Cho G là trọng tâm △ABC. Qua G vẽ đường thẳng song song AB và AC cắt BC lần lượt tại D, E. Chứng minh:
a)frac{BD}{BC}frac{1}{3}
b)BDDEEC
Bài 2: Đường thẳng d cắt các cạnh AB, AD và các đường chéo AC của hình bình hành ABCD lần lượt tại E, F, O.
Chứng minh: frac{AB}{AE}+frac{AD}{AF}frac{AC}{AO}
Bài 3: Cho A, B, C lần lượt nằm trên cạnh BC, AC, AB của △ABC. Biết rằng AA, BB, CC đồng quy tại M.
Chứng minh:frac{AM}{AM}frac{AB}{CB}+frac{AC}{BC}
Bài 4: Cho △ABC và trung tuyến...
Đọc tiếp
Bài 1: Cho G là trọng tâm △ABC. Qua G vẽ đường thẳng song song AB và AC cắt BC lần lượt tại D, E. Chứng minh:
a)\(\frac{BD}{BC}=\frac{1}{3}\)
b)\(BD=DE=EC\)
Bài 2: Đường thẳng d cắt các cạnh AB, AD và các đường chéo AC của hình bình hành ABCD lần lượt tại E, F, O.
Chứng minh: \(\frac{AB}{AE}+\frac{AD}{AF}=\frac{AC}{AO}\)
Bài 3: Cho A', B', C' lần lượt nằm trên cạnh BC, AC, AB của △ABC. Biết rằng AA', BB', CC' đồng quy tại M.
Chứng minh:\(\frac{AM}{A'M}=\frac{AB'}{CB'}+\frac{AC'}{BC'}\)
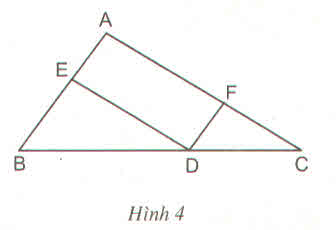
Bài 4: Cho △ABC và trung tuyến AM. Điểm O bất kỳ thuộc AM. F là giao điểm của BO và AC, E là giao điểm của OC và AB. Từ M kẻ đường thẳng song song OC cắt AB tại H và đường thẳng song song OB cắt AC tại K.Chứng minh:
a)EF//HK
b)EF//BC
Bài 5: Cho △ABC, kẻ đường thẳng song song BC cắt AB ở D và cắt AC ở E. Qua C kẻ Cx//AB và cắt DE ở G. Gọi H là giao điểm của AC và BG. Kẻ HI//AB (I thuộc BC).Chứng minh:
a)\(DA.EG=DB.DE\)
b)\(HC^2=HE.HA\)
c)\(\frac{1}{HI}=\frac{1}{AB}+\frac{1}{CG}\)