(CHI TIẾT) ( LÀM CẢ A VÀ B NHA)
Cho 1 người đi bộ từ A đến B dài 20km với vận tốc V1 = 5km/h . Ngườ này cứ đi 1h lại nghỉ 30p
a) Hỏi sau bao lâu thì người đó đến B và nghỉ mấy lần
b) 1 xe trở hàng liên tục trên tuyến A - B với V2 = 20km/h , sau khi đến A lại quay trở lại B và tiếp tục đi. Bt người đi bộ khởi hành từ lúc xe xuất phát từ B
Hỏi người đi bộ đã gặp xe hàng bao nhiên lần
a, Tgian đi hết sAB
\(t_1=\dfrac{s_{AB}}{v_1}=\dfrac{20}{5}=4h\)
Vì cứ 1h lại nghỉ 30p nên người đó nghỉ 3 lần
b, theo đề bài ta có chuyển động của người chở hàng
\(B\rightarrow A\rightarrow B\rightarrow A\)
=> Có nghĩa là đi 3 lần
Thời gian đi
\(t_2=\dfrac{s_{AB}}{v_2}=\dfrac{20.3}{20}=3h\)
Vì người chở hàng đi sAB ít hơn người đi bộ nên số lần bằng nhau cũng bằng số lượt xe chở hàng đi
Tham Khảo.
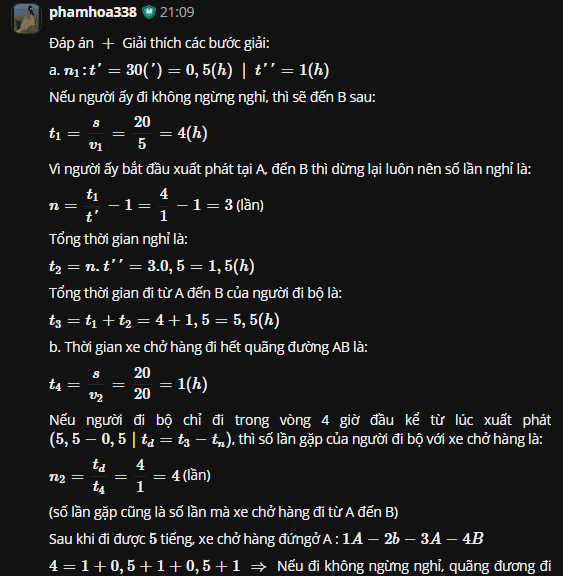
a. n1:t'=30(')=0,5(h)n1:t′=30(′)=0,5(h) ∣∣ t''=1(h)t′′=1(h)
Nếu người ấy đi không ngừng nghỉ, thì sẽ đến B sau:
t1=sv1=205=4(h)t1=sv1=205=4(h)
Vì người ấy bắt đầu xuất phát tại A, đến B thì dừng lại luôn nên số lần nghỉ là:
n=t1t'−1=41−1=3n=t1t′-1=41-1=3 (lần)
Tổng thời gian nghỉ là:
t2=n.t''=3.0,5=1,5(h)t2=n.t′′=3.0,5=1,5(h)
Tổng thời gian đi từ A đến B của người đi bộ là:
t3=t1+t2=4+1,5=5,5(h)t3=t1+t2=4+1,5=5,5(h)
b. Thời gian xe chở hàng đi hết quãng đường AB là:
t4=sv2=2020=1(h)t4=sv2=2020=1(h)
Nếu người đi bộ chỉ đi trong vòng 4 giờ đầu kể từ lúc xuất phát (5,5−0,5∣td=t3−tn)(5,5-0,5∣td=t3-tn), thì số lần gặp của người đi bộ với xe chở hàng là:
n2=tdt4=41=4n2=tdt4=41=4 (lần)
(số lần gặp cũng là số lần mà xe chở hàng đi từ A đến B)
Sau khi đi được 55 tiếng, xe chở hàng đứngở A : 1A−2b−3A−4B1A-2b-3A-4B
4=1+0,5+1+0,5+14=1+0,5+1+0,5+1 ⇒⇒ Nếu đi không ngừng nghỉ, quãng đương đi được của người đi bộ trong 3 tiếng tương đương với quãng đường người ấy đi trên thực tế (t_d +t_d +t_d=1+1+1=3)
Sau 44 tiếng người đi bộ đi được:
s1=v1.3=5.3=15(km)s1=v1.3=5.3=15(km)
Thời gian xe chở hàng và người đi bộ gặp nhau (TH* chuyển động không có điểm dừng, tính luôn người đi bộ chuyển động gặp xe chở hàng sau sau 4h)
tg=s1|v2+v1|=1520+5=0,6(h)tg=s1|v2+v1|=1520+5=0,6(h)
Khi ấy, người đi bộ đi được:
s2=v1.tg=5.0,6=3(km)s2=v1.tg=5.0,6=3(km)
⋅s<s1+s2=3+15=18(km)⋅s<s1+s2=3+15=18(km) ⇒⇒ Chửa đến AB
Điểm đó cách B một khoảng:
sB=s−(s1+s2)=20−18=2(km)sB=s-(s1+s2)=20-18=2(km)
Xe chở hàng đi được quãng đường kể từ khi gặp tại lần thứ 4:
s3=tg.v2=0,6.20=12(km)s3=tg.v2=0,6.20=12(km)
Nếu tính từ B, thì xe chở hàng kể từ lần thứ 4 gặp nhau đi được quãng đường cách B:
sB'=2+12=14(km)sB′=2+12=14(km)
Nhưng xe chở hàng còn phải về A, rồi từ A đến B với người đi bộ đến A trước khi gặp nhau lần thứ 5 (Giả thiết) nên không gặp thêm lần nữa, tức giả thiết không tồn tại | Tự chứng minh
(*Gợi ý: Khoảng cách tính từ A kể từ khi gặp nhau lần 4 đến khi người của người đi bộ luôn lớn hơn xe chở hàng)
Vậy Người đi bộ gặp người đi xe với số lần: n'=n3=4n′=n3=4(lần).