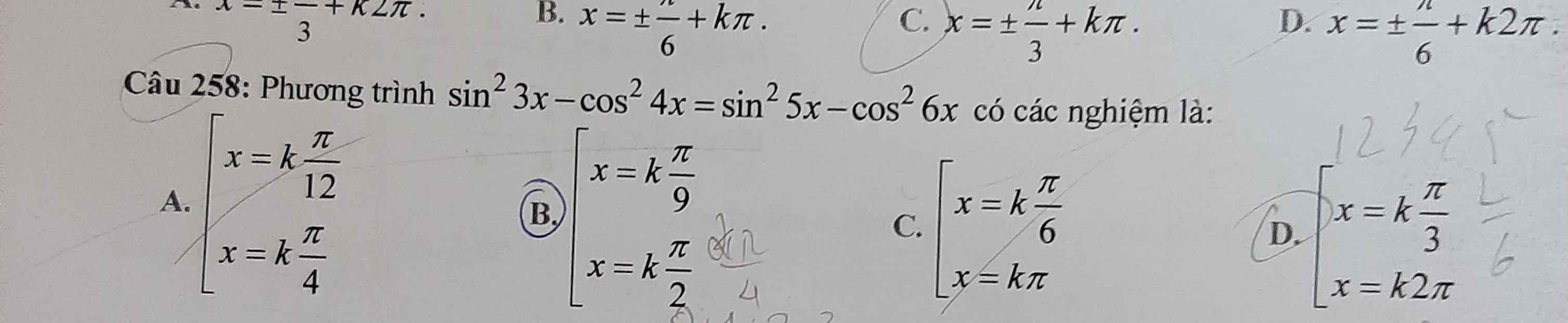\(-cos6x-cos8x=-cos10x-cos12x\)
\(\Leftrightarrow cos8x-cos12x+cos6x-cos10x=0\)
\(\Leftrightarrow2sin10x.sin2x+2sin8x.2x=0\)
\(\Leftrightarrow sin2x\left(sin10x+sin8x\right)=0\)
\(\Leftrightarrow2sin9x.cosx.sin2x=0\)
\(\Rightarrow\left[{}\begin{matrix}sin9x=0\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{9}\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
P/s: có thể loại ngay các đáp án A, C, D do:
\(\left[{}\begin{matrix}x=\dfrac{k\pi}{12}\\x=\dfrac{k\pi}{4}\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{k\pi}{12}\) (nghiệm \(\dfrac{k\pi}{4}\) là con của họ nghiệm \(\dfrac{k\pi}{12}\) khi thay \(k=3n\) vào \(\dfrac{k\pi}{12}\) ta sẽ được \(\dfrac{k\pi}{4}\))
\(\left[{}\begin{matrix}x=\dfrac{k\pi}{6}\\x=k\pi\end{matrix}\right.\) \(\Rightarrow x=\dfrac{k\pi}{6}\) tương tự như trên
\(\left[{}\begin{matrix}x=\dfrac{k\pi}{3}\\x=k2\pi\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{k\pi}{3}\)