Mấy bài này toàn áp dụng dãy tỉ số = nhau đó! Bn nên tưh thân vận động 1 chút chứ! Mk sẽ lm cho bn 2 bài bất kì!
Câu 12:
\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\) => \(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Áp dụng dãy tỉ số = nhau ta có:
\(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a+b-a+b}{c+d-c+d}=\dfrac{a+b+a-b}{c+d+c-d}\) = \(\dfrac{2a}{2c}=\dfrac{2b}{2d}\) =
= \(\dfrac{a}{c}=\dfrac{b}{d}\)
=> \(\dfrac{a}{b}=\dfrac{c}{d}\) => đpcm
Bài 8:
\(\dfrac{a_1}{a_2}=\dfrac{a_2}{a_3}=........=\dfrac{a_8}{a_9}=\dfrac{a_9}{a_1}\)
Vì \(a_1+a_2+a_3+.......+a_9\ne0\) nên áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a_1}{a_2}=\dfrac{a_2}{a_3}=........=\dfrac{a_8}{a_9}=\dfrac{a_9}{a_1}=\dfrac{a_1+a_2+a_3+.......+a_9}{a_2+a_3+.......+a_9+a_1}=1\)
\(\Rightarrow a_1=a_2=a_3=......=a_9\) (đpcm)
Chúc bạn học tốt!!!
Bài 7 :
Ta có :
\(\dfrac{a_1}{a_2}=\dfrac{a_2}{a_3}=....=\dfrac{a_{2008}}{a_{2009}}=\dfrac{a_1+a_2+....+a_{2008}}{a_2+a_3+....+a_{2009}}\)
\(\left(\dfrac{a_1}{a_2}\right)^{2008}=\left(\dfrac{a_1+a_2+.....+a_{2008}}{a_2+a_3+....+a_{2009}}\right)^{2008}\)
\(\dfrac{a_1}{a_2}.\dfrac{a_2}{a_3}......\dfrac{a_{2008}}{a_{2009}}=\left(\dfrac{a_1+a_2+.....+a_{2008}}{a_2+a_3+....+a_{2009}}\right)^{2008}\)
\(\dfrac{a_1}{a_{2009}}=\left(\dfrac{a_1+a_2+.....+a_{2008}}{a_2+a_3+....+a_{2009}}\right)^{2008}\)
Uầy .... cậu ko làm được cái j hết ak ![]()
Câu 18:
Ta có: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\) => \(\dfrac{2a+13b}{2c+13d}=\dfrac{3a-7b}{3c-7d}\)
Áp dụng dãy tỉ số = nhau ta có:
\(\dfrac{2a+13b}{2c+13d}=\dfrac{3a-7b}{3c-7d}\) = \(\dfrac{6a+39b}{6c+39d}=\dfrac{6a-14b}{6c-14b}\)
= \(\dfrac{6a+39b-6a+14b}{6c+39d-6c+14d}\) = \(\dfrac{53b}{53d}\) = \(\dfrac{b}{d}\) (1)
Ta lại có: \(\dfrac{2a+13b}{2c+13d}=\dfrac{3a-7b}{3c-7d}\) = \(\dfrac{14a+91b}{14c+91d}=\dfrac{39a-91b}{39c-91d}\)
= \(\dfrac{14a+91b+39a-91b}{14c+91d+39c-91d}\) = \(\dfrac{53a}{53c}\) = \(\dfrac{a}{c}\) (2)
Từ (1); (2) => \(\dfrac{a}{c}=\dfrac{b}{d}\) => \(\dfrac{a}{b}=\dfrac{c}{d}\) => đpcm
Bài 11:
Ta có: \(a^2=bc\Leftrightarrow a.a=b.c\)
\(\Rightarrow\dfrac{b}{a}=\dfrac{a}{c}=\dfrac{b+a}{a+c}=\dfrac{b-a}{a-c}\)
\(\Rightarrow\dfrac{b+a}{b-a}=\dfrac{a+c}{a-c}\)
Vậy có thể viết dưới dạng....














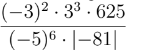 cái bài n mk biết làm mà do muốn rõ hơn nên các bn làm chi tiết hộ mk nha ! Cảm ơn nhiều !
cái bài n mk biết làm mà do muốn rõ hơn nên các bn làm chi tiết hộ mk nha ! Cảm ơn nhiều !