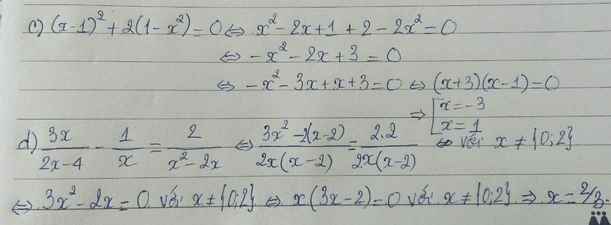c) \(\left(x-1\right)^2+2\left(1-x^2\right)=0\)
\(\left(x-1\right)^2-2\left(x-1\right)\left(x+1\right)=0\)
\(\left(x-1\right)\left(x-1-2x-2\right)=0\)
\(\left(x-1\right)\left(-x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
d) \(\dfrac{3x}{2\left(x-2\right)}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)
\(\dfrac{3x^2-2\left(x-2\right)}{2x\left(x-2\right)}=\dfrac{4}{2x\left(x-2\right)}\left(đk:x\ne0;2\right)\)
\(3x^2-2x+4=4\)
\(x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
c, \(\left(x-1\right)\left(x+1\right)+2\left(1-x\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)+\left(2-2x\right)\left(x+1\right)=0\Leftrightarrow\left(x+1\right)\left(-x+1\right)=0\Leftrightarrow x=-1;x=1\)
d, đk x khác 0 ; 2\(\Rightarrow3x^2-2\left(x-2\right)=4\Leftrightarrow3x^2-2x=0\Leftrightarrow x\left(3x-2\right)=0\Leftrightarrow x=0\left(ktm\right);x=\dfrac{2}{3}\)
c.
\(\left(x-1\right)^2+2\left(1-x^2\right)=0\\ \Leftrightarrow x^2-2x+1+2-2x^2=0\\ \Leftrightarrow-x^2-2x+3=0\\ \Leftrightarrow x\left(-x-2+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)