`#3107.\text{DN}`
c)
\(\dfrac{27^3+9^3+9^4}{37}\)
\(=\dfrac{9^3\cdot3^3+9^3+9^4}{37}\\ =\dfrac{9^3\cdot\left(3^3+1\right)+9^4}{37}\\ =\dfrac{9^3\cdot28+9^4}{37}\\ =\dfrac{9^3\cdot\left(28+9\right)}{37}\\ =\dfrac{9^3\cdot37}{37}\\ =9^3=729\)
d)
\(\dfrac{10^9\cdot81^{10}}{8^4\cdot25^5\cdot9^{10}}\)
\(=\dfrac{2^9\cdot5^9\cdot\left(3^2\right)^{10}}{\left(2^3\right)^4\cdot\left(5^2\right)^5\cdot\left(3^2\right)^{10}}\)
\(=\dfrac{2^9\cdot5^9\cdot3^{20}}{2^{12}\cdot5^{10}\cdot3^{20}}\)
\(=\dfrac{1}{2^3\cdot5}\\ =\dfrac{1}{8\cdot5}\\ =\dfrac{1}{40}\)
e)
\(\dfrac{9^4\cdot4^5\cdot25^3}{8^3\cdot27^2\cdot5^7}\)
\(=\dfrac{\left(3^2\right)^4\cdot\left(2^2\right)^5\cdot\left(5^2\right)^3}{\left(2^3\right)^3\cdot\left(3^3\right)^2\cdot5^7}\\ =\dfrac{3^8\cdot2^{10}\cdot5^6}{2^9\cdot3^6\cdot5^7}\\ =\dfrac{3^2\cdot2}{5}\\ =\dfrac{18}{5}\)
f)
\(\dfrac{5}{4}\cdot\dfrac{8}{15}+\dfrac{-5}{16}\cdot\dfrac{8}{15}-1\)
\(=\dfrac{8}{15}\cdot\left(\dfrac{5}{4}-\dfrac{5}{16}\right)-1\\ =\dfrac{8}{15}\cdot\dfrac{15}{16}-1\\ =\dfrac{8}{16}-1\\ =\dfrac{1}{2}-1\\ =-\dfrac{1}{2}\)
g)
\(4\dfrac{5}{9}\div\left(-\dfrac{5}{7}\right)+5\dfrac{4}{9}\div\left(-\dfrac{5}{7}\right)\\ =4\dfrac{5}{9}\cdot\left(-\dfrac{7}{5}\right)+5\dfrac{4}{9}\cdot\left(-\dfrac{7}{5}\right)\\ =\left(-\dfrac{7}{5}\right)\cdot\left(4\dfrac{5}{9}+5\dfrac{4}{9}\right)\\ =\left(-\dfrac{7}{5}\right)\cdot\left[\left(4+5\right)+\left(\dfrac{5}{9}+\dfrac{4}{9}\right)\right]\\ =\left(-\dfrac{7}{5}\right)\cdot\left(9+1\right)\\ =\left(-\dfrac{7}{5}\right)\cdot10\\ =-14\)
h)
\(\dfrac{2}{7}\cdot\dfrac{8}{19}+\dfrac{5}{7}\cdot\dfrac{8}{19}\\ =\dfrac{8}{19}\cdot\left(\dfrac{2}{7}+\dfrac{5}{7}\right)\\ =\dfrac{8}{19}\cdot\dfrac{7}{7}\\ =\dfrac{8}{19}\cdot1\\ =\dfrac{8}{19}\)
i)
\(\dfrac{9}{10}\cdot\dfrac{23}{11}-\dfrac{1}{11}\cdot\dfrac{9}{10}+\dfrac{9}{10}\\ =\dfrac{9}{10}\cdot\left(\dfrac{23}{11}-\dfrac{1}{11}+1\right)\\ =\dfrac{9}{10}\cdot\left(\dfrac{23}{11}-\dfrac{1}{11}+\dfrac{11}{11}\right)\\ =\dfrac{9}{10}\cdot\left(\dfrac{23-1+11}{11}\right)\\ =\dfrac{9}{10}\cdot\dfrac{33}{11}\\ =\dfrac{9}{10}\cdot3\\ =\dfrac{27}{10}\)

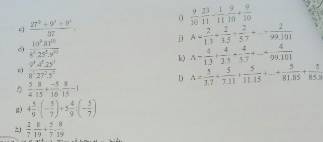 ; ;;;bài đây nhé các câu
; ;;;bài đây nhé các câu












 các ban làm mấy câu khoanh tròn giúp mình với nhé mấy câu lũy thừa mình không hiểu lắm
các ban làm mấy câu khoanh tròn giúp mình với nhé mấy câu lũy thừa mình không hiểu lắm
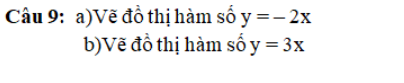

 mình bài 9,10,11 nhé các bạn thân yêu
mình bài 9,10,11 nhé các bạn thân yêu