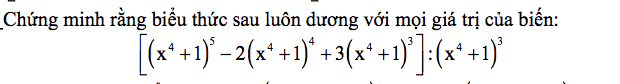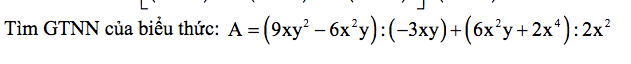Question

bài 1:

bài 2: 

Answer 1

\(Biểu.thức=\left(x^4-1\right)^2-2\left(x^4-1\right)+3=\left(x^4-1\right)^2+2\left(x^4-1\right)+1+2\\ =\left(x^4-1-1\right)^2+2=\left(x^4-2\right)^2+2\ge2>0\)

Answer 2

\(2,\\ A=-3y+2x+3y+2x^2=2x^2+2x\\ A=2\left(x^2+x+\dfrac{1}{4}-\dfrac{1}{4}\right)=2\left(x+\dfrac{1}{2}\right)^2-\dfrac{1}{2}\ge-\dfrac{1}{2}\\ A_{min}=-\dfrac{1}{2}\Leftrightarrow x=-\dfrac{1}{2};y\in R\)