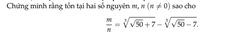Lời giải:
Ta có: \(4^x+2^x=4x+2\) \(\Leftrightarrow 4^x+2^x-4x-2=0\)
Đặt \(f(x)=4^x+2^x-4x-2\)
\(\Rightarrow f'(x)=\ln 4.4^x+\ln 2.2^x-4\)
\(f'(x)=\ln 4(2^x)^2+\ln 2.2^x-4=0\Leftrightarrow \) \(\left[{}\begin{matrix}2^x\approx-1.96\left(vl\right)\\2^x=1.47\end{matrix}\right.\)
\(\Leftrightarrow x\approx \log_2(1.47)\)
Lập bảng biến thiên:

Từ bảng biến thiên ta suy ra pt \(f(x)=0\) có nghiệm \(x=\left\{0;1\right\}\)