1. Cho tam giác ABC ( góc A = 90 độ ) , BD là tia phân giác của góc B ( D thuộc AC ). Trên tia BC lấy điểm E sao cho BA = BE.
a, CM: DE vuông góc với BE
b, CM: BD là đường trung trực của AE.
c, Kẻ AH vuông góc với BC. So sánh EH và EC
2. Cho tam giác ABC ( góc a = 90 độ ), AB = 8cm, AC = 6cm.
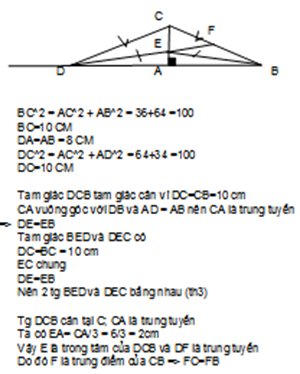
a, BC =?
b, Trên cạnh AC lấy điểm E sao cho AE = 2cm, trên tia đối của tia AB lấy điểm D sao cho AD = AB
c, CM: DE đi qua trung điểm cạnh BC
Bài 1:
a) Xét hai tam giác ABD và EBD có:
AB = EB (gt)
\(\widehat{ABD}=\widehat{EBD}\) (gt)
BD: cạnh chung
Vậy: \(\Delta ABD=\Delta EBD\left(c-g-c\right)\)
Suy ra: \(\widehat{BAD}=\widehat{BED}\) (hai góc tương ứng)
Mà \(\widehat{BAD}=90^o\)
Do đó \(\widehat{BED}=90^o\) hay DE \(\perp\) BE (đpcm).
b) Vì AB = EB (gt)
\(\Rightarrow\Delta ABE\) cân tại B
\(\Rightarrow\) BD là đường phân giác đồng thời là đường trung trực
Vậy BD là đường trung trực của AE (đpcm).
c) Ta có AH // DE (cùng vuông góc với BC)
\(\Rightarrow\widehat{HAD}=\widehat{EDC}\) (hai góc đồng vị bằng nhau)
Mà \(\widehat{HAE}< \widehat{HAD}\left(\widehat{HAE}+\widehat{EAD}=\widehat{HAD}\right)\)
Suy ra \(\widehat{HAE}< \widehat{EDC}\)
Do đó EH < EC (đpcm).
a) Xét hai tam giác ABD và EBD có:
AB = EB (gt)
ABDˆ=EBDˆABD^=EBD^ (gt)
BD: cạnh chung
Vậy: ΔABD=ΔEBD(c−g−c)ΔABD=ΔEBD(c−g−c)
Suy ra: BADˆ=BEDˆBAD^=BED^ (hai góc tương ứng)
Mà BADˆ=90oBAD^=90o
Do đó BEDˆ=90oBED^=90o hay DE ⊥⊥ BE (đpcm).
b) Vì AB = EB (gt)
⇒ΔABE⇒ΔABE cân tại B
⇒⇒ BD là đường phân giác đồng thời là đường trung trực
Vậy BD là đường trung trực của AE (đpcm).
c) Ta có AH // DE (cùng vuông góc với BC)
⇒HADˆ=EDCˆ⇒HAD^=EDC^ (hai góc đồng vị bằng nhau)
Mà HAEˆ<HADˆ(HAEˆ+EADˆ=HADˆ)HAE^<HAD^(HAE^+EAD^=HAD^)
Suy ra HAEˆ<EDCˆHAE^<EDC^
Do đó EH < EC (đpcm).
a) Xét hai tam giác ABD và EBD có:
AB = EB (gt)
ABDˆ=EBDˆABD^=EBD^ (gt)
BD: cạnh chung
Vậy: ΔABD=ΔEBD(c−g−c)ΔABD=ΔEBD(c−g−c)
Suy ra: BADˆ=BEDˆBAD^=BED^ (hai góc tương ứng)
Mà BADˆ=90oBAD^=90o
Do đó BEDˆ=90oBED^=90o hay DE ⊥⊥ BE (đpcm).
b) Vì AB = EB (gt)
⇒ΔABE⇒ΔABE cân tại B
⇒⇒ BD là đường phân giác đồng thời là đường trung trực
Vậy BD là đường trung trực của AE (đpcm).
c) Ta có AH // DE (cùng vuông góc với BC)
⇒HADˆ=EDCˆ⇒HAD^=EDC^ (hai góc đồng vị bằng nhau)
Mà HAEˆ<HADˆ(HAEˆ+EADˆ=HADˆ)HAE^<HAD^(HAE^+EAD^=HAD^)
Suy ra HAEˆ<EDCˆHAE^<EDC^
Do đó EH < EC (đpcm).