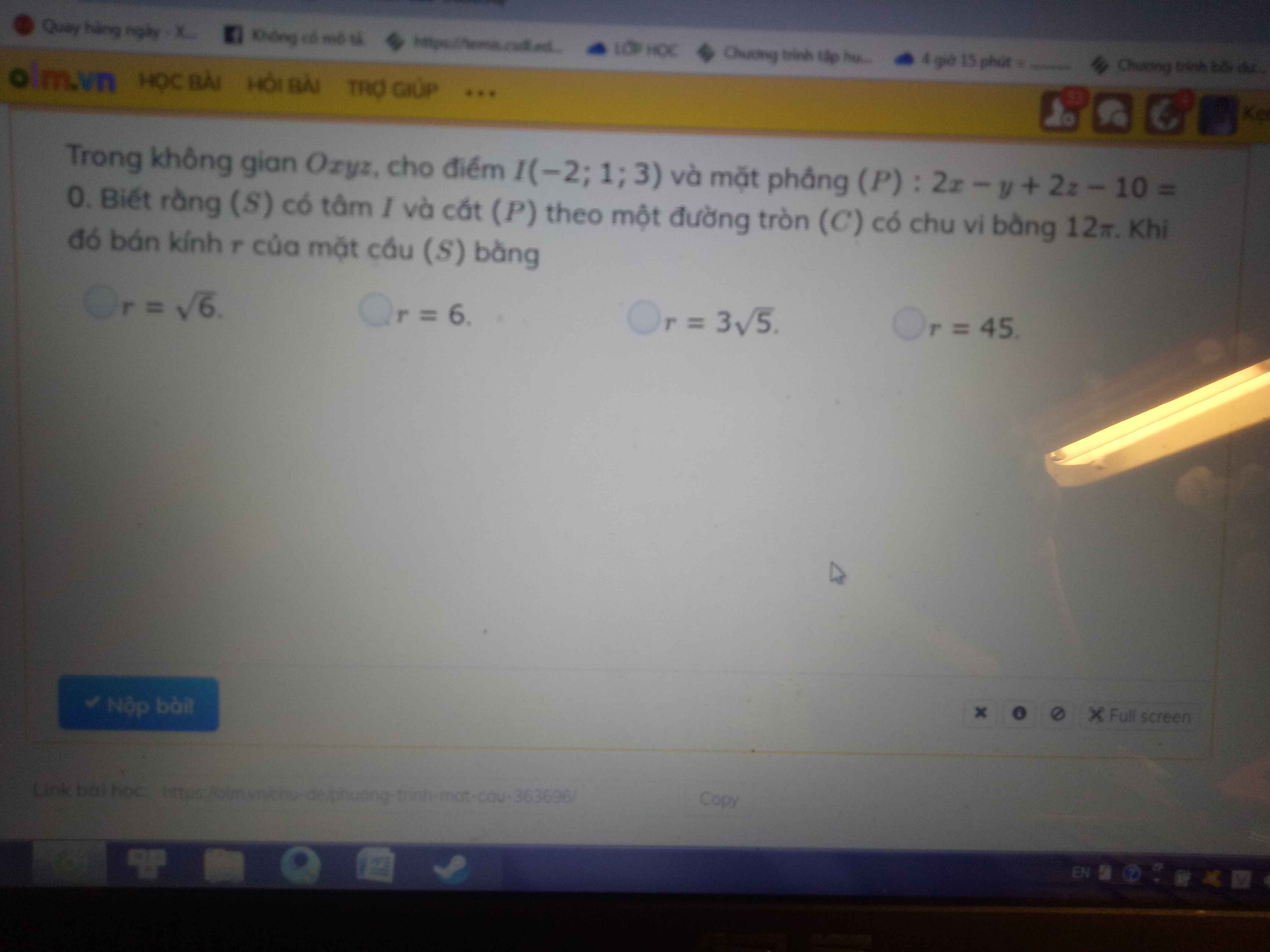
Gọi R là bán kính (C) \(\Rightarrow2\pi R=12\pi\Rightarrow R=6\)
Gọi \(J\) là tâm (C) \(\Rightarrow IJ\perp\left(P\right)\Rightarrow IJ=d\left(I;\left(P\right)\right)\)
\(d\left(I;\left(P\right)\right)=\dfrac{\left|2.\left(-2\right)-1.1+2.3-10\right|}{\sqrt{2^2+\left(-1\right)^2+2^2}}=3\)
\(\Rightarrow IJ=3\)
Áp dụng định lý Pitago:
\(r^2=IJ^2+R^2=45\Rightarrow r=3\sqrt{5}\)
Đường tròn (C) có bán kính R = 6.
d(I,(P))=3.
Mặt cầu cắt mặt phẳng theo một đường tròn
(C) nên có bán kính:
r=\(\sqrt{R^2+(d(I,(P)))^2 } =3\sqrt{5}
\)(P theo một đường tròn (C) nên có bán kính:(S) cắt mặt phẳng (P)