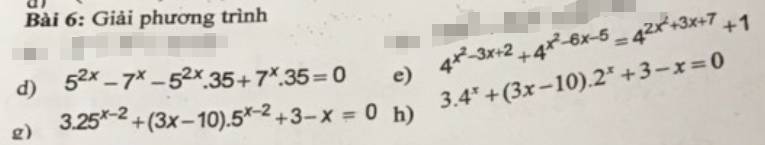d: \(5^{2x}-7^x-5^{2x}\cdot35+7^x\cdot35=0\)
=>\(\left(5^{2x}-7^x\right)-35\left(5^{2x}-7^x\right)=0\)
=>\(\left(5^{2x}-7^x\right)\cdot\left(-34\right)=0\)
=>\(5^{2x}-7^x=0\)
=>\(5^{2x}=7^x\)
=>\(25^x=7^x\)
=>\(\left(\dfrac{7}{25}\right)^x=1\)
=>x=0
g: \(3\cdot25^{x-2}+\left(3x-10\right)\cdot5^{x-2}+3-x=0\)
=>\(3\cdot\left(5^{x-2}\right)^2-5^{x-2}+\left(3x-9\right)\cdot5^{x-2}-\left(x-3\right)=0\)
=>\(5^{x-2}\left(3\cdot5^{x-2}-1\right)+\left(x-3\right)\left(3\cdot5^{x-2}-1\right)=0\)
=>\(\left(5^{x-2}+x-3\right)\left(3\cdot5^{x-2}-1\right)=0\)
=>\(\left[{}\begin{matrix}5^{x-2}+x-3=0\\3\cdot5^{x-2}-1=0\end{matrix}\right.\)
TH1: \(5^{x-2}+x-3=0\)
Đặt \(A\left(x\right)=5^{x-2}+x-3\)
=>\(A\left(x\right)=\dfrac{1}{25}\cdot5^x+x-3\)
=>\(A'\left(x\right)=\dfrac{1}{25}\cdot5^x\cdot ln5+1>0\)
=>A(x) luôn đồng biến trên R
=>A(x)=0 khi x=2
Th2: \(3\cdot5^{x-2}-1=0\)
=>\(5^{x-2}=\dfrac{1}{3}\)
=>\(x-2=log_5\dfrac{1}{3}\)
=>\(x=2+log_5\left(\dfrac{1}{3}\right)\)
h: \(3\cdot4^x+\left(3x-10\right)\cdot2^x+3-x=0\)
=>\(3\cdot4^x-2^x+\left(3x-9\right)\cdot2^x-\left(x-3\right)=0\)
=>\(2^x\left(3\cdot2^x-1\right)+\left(x-3\right)\left(3\cdot2^x-1\right)=0\)
=>\(\left(3\cdot2^x-1\right)\left(2^x+x-3\right)=0\)
TH1: \(3\cdot2^x-1=0\)
=>\(2^x=\dfrac{1}{3}\)
=>\(x=log\left(\dfrac{1}{3}\right)\)
TH2: \(2^x+x-3=0\)
Đặt \(B\left(x\right)=2^x+x-3\)
=>\(B'\left(x\right)=2^x\cdot ln3+1>0\)
=>B(x) luôn đồng biến trên R
=>B(x)=0 khi x=1