Đề 4:
Bài 2: GPT:
a) \(3\sqrt{16x-32}=36+\sqrt{9x-18}\left(x\ge2\right)\)
\(\Leftrightarrow3\cdot4\sqrt{x-2}=36+3\sqrt{x-2}\)
\(\Leftrightarrow12\sqrt{x-2}=36+3\sqrt{x-2}\)
\(\Leftrightarrow12\sqrt{x-2}-3\sqrt{x-2}=36\)
\(\Leftrightarrow9\sqrt{x-2}=36\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=4^2\)
\(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\left(tm\right)\)
b) \(\sqrt{x^2-2x\sqrt{6}+6}-\sqrt{6}=0\left(x\in R\right)\)
\(\Leftrightarrow\sqrt{x^2-2x\sqrt{6}+6}=\sqrt{6}\)
\(\Leftrightarrow\sqrt{x^2-2\cdot x\cdot\sqrt{6}+\left(\sqrt{6}\right)^2}=\sqrt{6}\)
\(\Leftrightarrow\sqrt{\left(x-\sqrt{6}\right)^2}=\sqrt{6}\)
\(\Leftrightarrow\left|x-\sqrt{6}\right|=\sqrt{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\sqrt{6}=\sqrt{6}\left(x\ge\sqrt{6}\right)\\x-\sqrt{6}=-\sqrt{6}\left(x< \sqrt{6}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\sqrt{6}\left(tm\right)\\x=0\left(tm\right)\end{matrix}\right.\)
Bài 1:(Đề 5)
a: \(\dfrac{3}{2}\sqrt{12}+\sqrt{75}-\sqrt{300}+\sqrt{27}\)
\(=\dfrac{3}{2}\cdot2\sqrt{3}+5\sqrt{3}-10\sqrt{3}+3\sqrt{3}\)
\(=3\sqrt{3}-2\sqrt{3}=\sqrt{3}\)
b: \(\sqrt{16-6\sqrt{7}}-\sqrt{\left(2-\sqrt{7}\right)^2}\)
\(=\sqrt{9-2\cdot3\cdot\sqrt{7}+7}-\sqrt{\left(\sqrt{7}-2\right)^2}\)
\(=\sqrt{\left(3-\sqrt{7}\right)^2}-\left|\sqrt{7}-2\right|\)
\(=\left|3-\sqrt{7}\right|-\left(\sqrt{7}-2\right)\)
\(=3-\sqrt{7}-\sqrt{7}+2=5-2\sqrt{7}\)
Câu 4(Đề 4)
a: 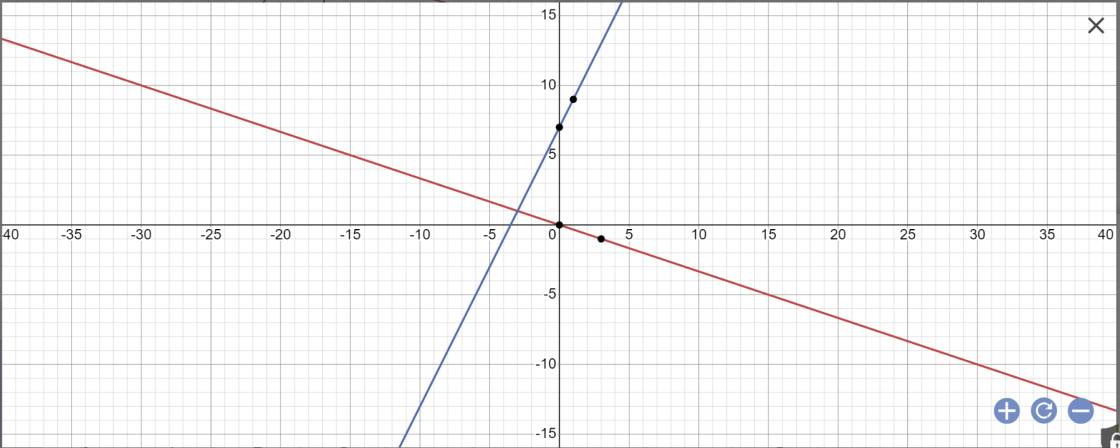
b: Phương trình hoành độ giao điểm là:
\(2x+7=-\dfrac{1}{3}x\)
=>\(2x+\dfrac{1}{3}x=-7\)
=>\(x\cdot\dfrac{7}{3}=-7\)
=>x=-3
Thay x=-3 vào y=-1/3x, ta được:
\(y=-\dfrac{1}{3}\cdot\left(-3\right)=1\)
















