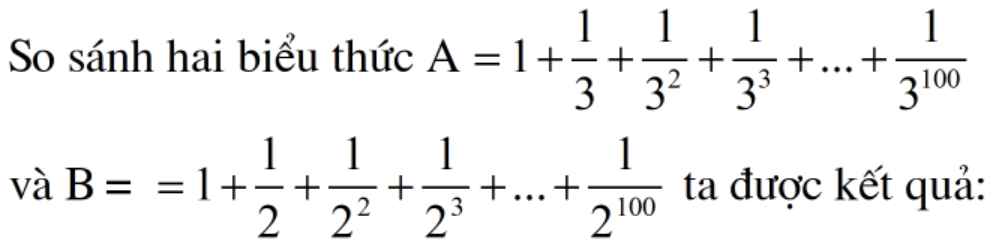Bài 1:
\(B\left(6\right)=\left\{0;6;12;18;24;30;36;42;48;54;60;...\right\}\)
\(B\left(12\right)=\left\{0;12;24;36;48;60;72;84;...\right\}\)
Ta có:
\(6=2\cdot3\)
\(12=2^2\cdot3\)
\(42=2\cdot3\cdot7\)
\(\Rightarrow BCNN\left(6;12;42\right)=2^2\cdot3\cdot7=84\)
\(\Rightarrow BC\left(6;12;42\right)=\left\{0;84;168;252;...\right\}\)
Bài 2:
a: \(24=2^3\cdot3;10=2\cdot5\)
=>\(BCNN\left(10;24\right)=2^3\cdot3\cdot5=120\)
b: \(8=2^3;12=2^2\cdot3;15=3\cdot5\)
=>\(BCNN\left(8;12;15\right)=2^3\cdot3\cdot5=120\)
Bài 3:
\(120=2^3\cdot15;86=2\cdot43\)
=>\(BCNN\left(120;86\right)=2^3\cdot15\cdot43=5160\)
\(a⋮120;a⋮86\)
=>\(a\in BC\left(120;86\right)\)
mà a nhỏ nhất khác 0
nên a=BCNN(120;86)
=>a=5160