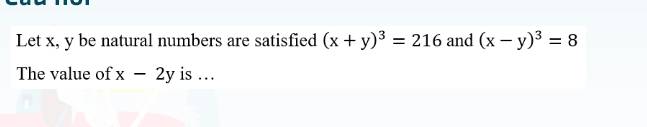Ta có:
\(\left(x+y\right)^3=216\)
\(\Rightarrow\left(x+y\right)^3=6^3\)
\(\Rightarrow x+y=6\) (1)
___________
\(\left(x-y\right)^3=8\)
\(\Rightarrow\left(x-y\right)^3=2^3\)
\(\Rightarrow x-y=2\) (2)
Từ (1) và (2) ta có:
\(x=\left(6+2\right):2=4\)
\(\Rightarrow y=4-2=2\)
Vậy giá trị của x - 2y là:
\(x-2y=4-2\cdot2=0\)
\(\left(x+y\right)^3=216\)
=>x+y=6
\(\left(x-y\right)^3=8\)
=>x-y=2
mà x+y=6
nên \(x=\dfrac{2+6}{2}=4;y=6-4=2\)
\(x-2y=4-2\cdot2=0\)
Ta có:
\((x+y)^3=216\\\Rightarrow (x+y)^3=6^3\\\Rightarrow x+y=6 ^{(1)}\)
Lại có:
\((x-y)^3=8\\\Rightarrow (x-y)^3=2^3\\\Rightarrow x-y=2^{(2)}\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\left(x+y\right)+\left(x-y\right)=6+2\)
\(\Rightarrow x+y+x-y=8\)
\(\Rightarrow2x=8\)
\(\Rightarrow x=8:2=4\)
Thay \(x=4\) vào \(\left(1\right)\), ta được:
\(4+y=6\)
\(\Rightarrow y=6-4=2\)
Khi đó: \(x-2y=4-2\cdot2\)
\(=4-4=0\)
Vậy: ...
\(Toru\)
(x + y)³ = 216 ⇒ x + y = 6
(x - y)³ = 8 ⇒ x - y = 2
⇒ x = (6 + 2) : 2 = 4
⇒ y = (6 - 2) : 2 = 2
⇒ x - 2y = 4 - 2.2 = 0
Ta có:
(x+y)3=216(�+�)3=216
⇒(x+y)3=63⇒(�+�)3=63
⇒x+y=6⇒�+�=6 (1)
___________
(x−y)3=8(�−�)3=8
⇒(x−y)3=23⇒(�−�)3=23
⇒x−y=2⇒�−�=2 (2)
Từ (1) và (2) ta có:
x=(6+2):2=4�=(6+2):2=4
⇒y=4−2=2⇒�=4−2=2
Vậy giá trị của x - 2y là:
x−2y=4−2⋅2=0