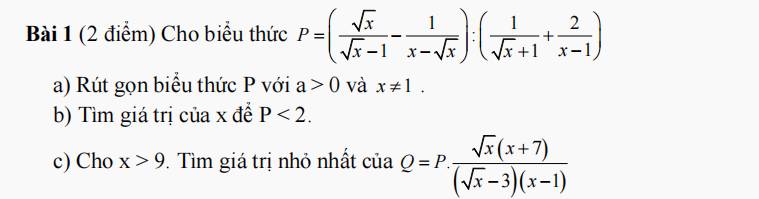a) \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)
\(P=\left[\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\)
\(P=\left[\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\)
\(P=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(P=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(P=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\left(\sqrt{x}-1\right)\)
\(P=\dfrac{x-1}{\sqrt{x}}\)
b) \(P< 2\) khi và chỉ khi:
\(\dfrac{x-1}{\sqrt{x}}< 2\)
\(\Leftrightarrow\dfrac{x-1-2\sqrt{x}}{\sqrt{x}}< 0\)
\(\Leftrightarrow x-2\sqrt{x}-1< 0\)
\(\Leftrightarrow x-2\sqrt{x}+1-2< 0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2-2< 0\)
\(\Leftrightarrow\sqrt{x}-1< 4\)
\(\Leftrightarrow x< 25\)
Kết hợp với đk:
\(0< x< 25\)
c) Ta có:
\(Q=P\cdot\dfrac{\sqrt{x}\left(x+7\right)}{\left(\sqrt{x}-3\right)\left(x-1\right)}\)
\(Q=\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(x+7\right)}{\left(\sqrt{x}-3\right)\left(x-1\right)}\)
\(Q=\dfrac{x+7}{\sqrt{x}-3}\)
\(Q=\dfrac{x-9+16}{\sqrt{x}-3}=\sqrt{x}+3+\dfrac{16}{\sqrt{x}-3}=\sqrt{x}-3+\dfrac{16}{\sqrt{x}-3}+6\)
Theo BĐT Cauchy cho các số dương ta có:
\(\sqrt{x}-3+\dfrac{16}{\sqrt{x}-3}\ge2\sqrt{\left(\sqrt{x}-3\right)\cdot\dfrac{16}{\sqrt{x}-3}}=2\sqrt{16}=2\cdot4=8\)
\(\Rightarrow\sqrt{x}-3+\dfrac{16}{\sqrt{x}-3}+6\ge8+6=14\)
Dấu "=" xảy ra khi: \(x=49\)
Vậy \(Q_{min}=14\) khi \(x=49\)