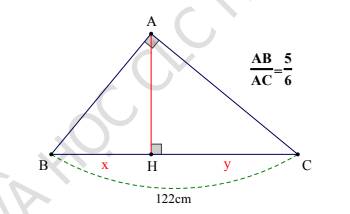
Ta có: \(BC^2=AB^2+AC^2\) (định lí pitago)
\(\Rightarrow122^2=\left(\dfrac{5AC}{6}\right)^2+AC^2\) (do \(\dfrac{AB}{AC}=\dfrac{5}{6}\))
\(\Rightarrow AC=12\sqrt{61}cm\) (do \(AC>0\))
Ta có: \(AC^2=CH.BC\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{\left(12\sqrt{61}\right)^2}{122}=72cm\)
\(\Rightarrow y=72cm\)
Lại có: \(BH+HC=BC\)
\(\Rightarrow BH=BC-HC=122-72=50cm\)
\(\Rightarrow x=50cm\)