Lời giải:
Gọi biểu thức vế trái là $A$
Áp dụng BĐT AM-GM:
$\frac{a^3}{1+b^2}+\frac{a(b^2+1)}{4}\geq a^2$
$\frac{b^3}{1+a^2}+\frac{b(a^2+1)}{4}\geq b^2$
$\Rightarrow A+\frac{a(b^2+1)+b(a^2+1)}{4}\geq a^2+b^2$
$\Leftrightarrow A+\frac{ab(a+b)+a+b}{4}\geq a^2+b^2$
$\Leftrightarrow A+\frac{a+b}{2}\geq a^2+b^2$
Áp dụng BĐT AM-GM:
$a^2+1\geq 2a$
$b^2+1\geq 2b$
$\Rightarrow a^2+b^2\geq 2(a+b)-2$
$\Rightarrow A+\frac{a+b}{2}\geq a^2+b^2\geq 2(a+b)-2$
$\Rightarrow A\geq \frac{3}{2}(a+b)-2\geq \frac{3}{2}.2\sqrt{ab}-2=3-2=1$
Ta có đpcm.
Dấu "=" xảy ra khi $a=b=1$

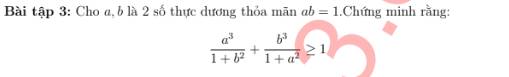
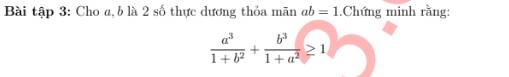












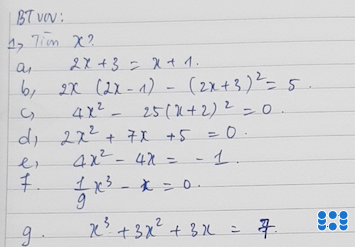

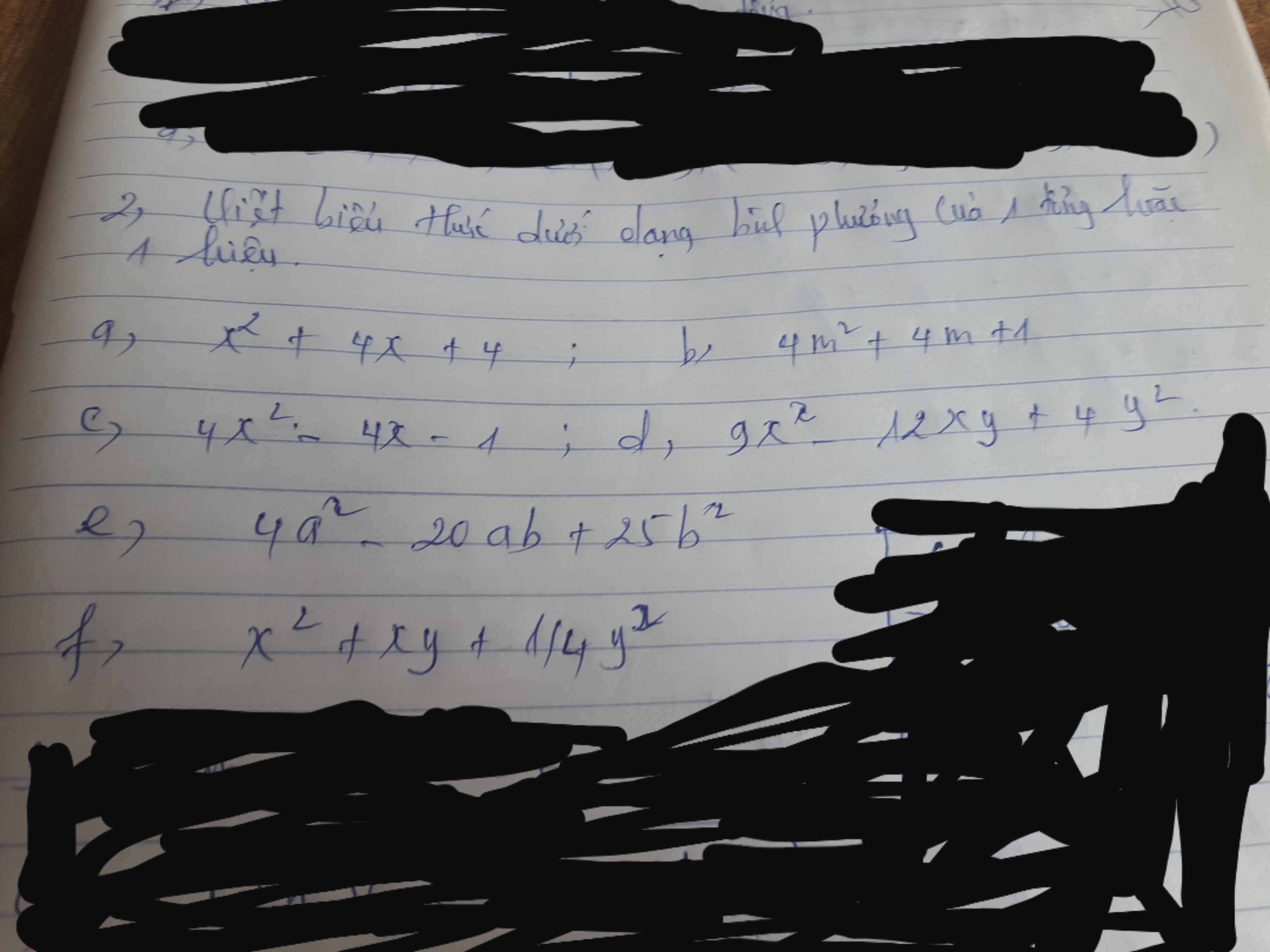



 giải thích giùm mình với
giải thích giùm mình với