Bài 7 :
\(a,A=\left(\dfrac{1}{x^2+x}-\dfrac{2-x}{x+1}\right).\dfrac{3x}{1-2x+x^2}\left(x\ne0;x\ne\pm1\right)\)
\(=\left(\dfrac{1}{x\left(x+1\right)}-\dfrac{2-x}{x+1}\right).\dfrac{3x}{\left(1-x\right)^2}\)
\(=\dfrac{1-x\left(2-x\right)}{x\left(x+1\right)}.\dfrac{3x}{\left(1-x\right)^2}\)
\(=\dfrac{1-2x+x^2}{x\left(x+1\right)}.\dfrac{3x}{\left(1-x\right)^2}\)
\(=\dfrac{\left(1-x\right)^2}{x\left(x+1\right)}.\dfrac{3x}{\left(1-x\right)^2}\)
\(=\dfrac{3}{x+1}\)
\(b,\) Để \(A=\dfrac{1}{673}\) thì :
\(\dfrac{3}{x+1}=\dfrac{1}{673}\)
\(\Leftrightarrow3.673=x+1\)
\(\Leftrightarrow x+1=2019\)
\(\Leftrightarrow x=2018\)
Bài 7:
a: \(A=\left(\dfrac{1}{x\left(x+1\right)}+\dfrac{x-2}{x+1}\right)\cdot\dfrac{3x}{\left(x-1\right)^2}\)
\(=\dfrac{1+x^2-2x}{x\left(x+1\right)}\cdot\dfrac{3x}{\left(x-1\right)^2}=\dfrac{3}{x+1}\)
b: Để A=1/673 thì 3/x+1=1/673
=>x+1=2019
=>x=2018
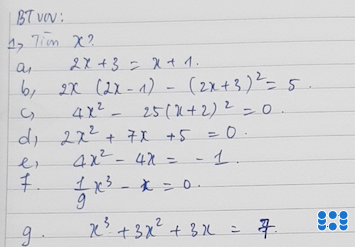
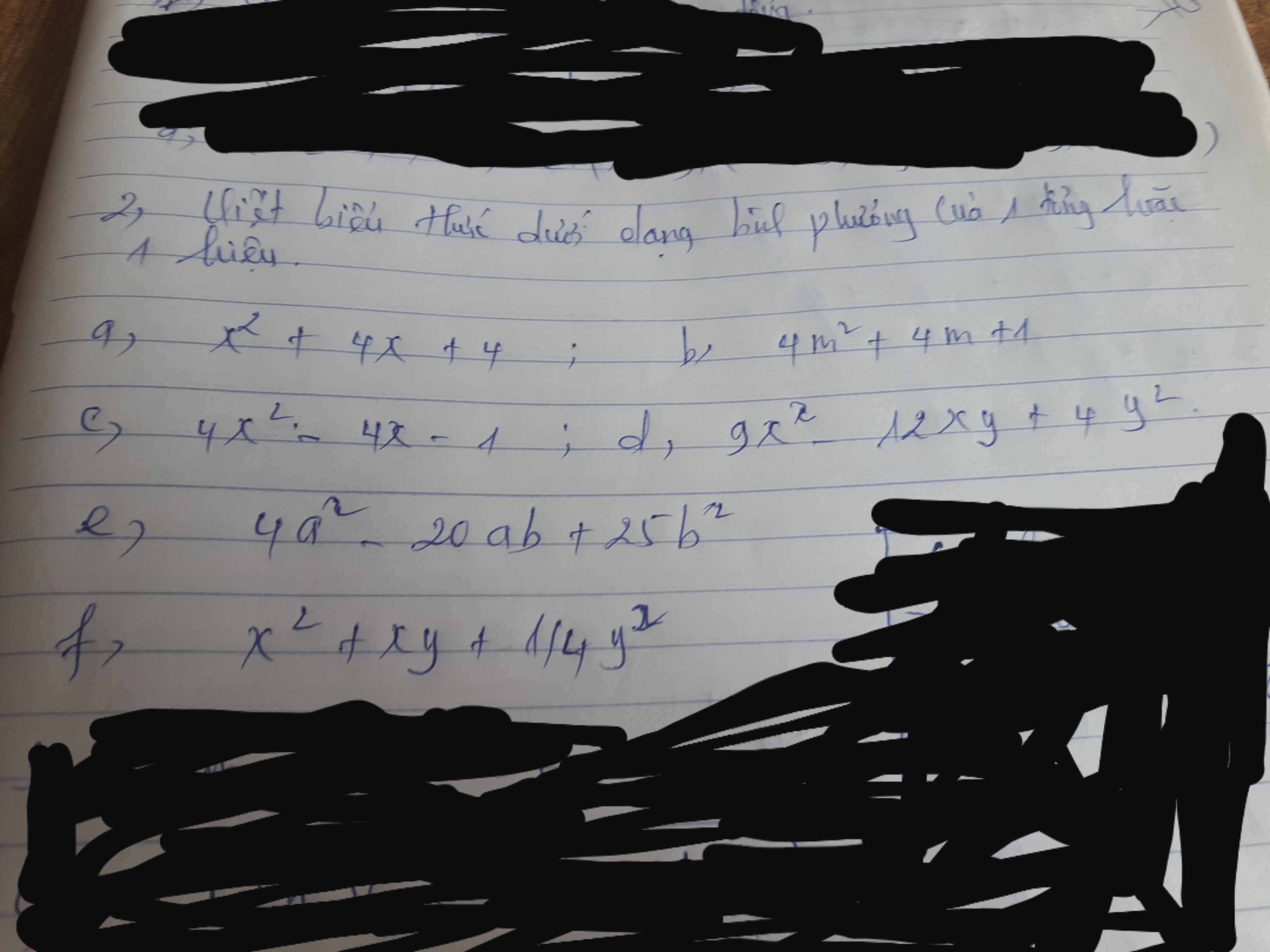
giải thích giùm mình với