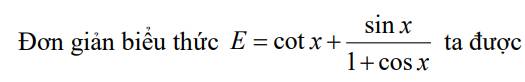\(=\dfrac{cosx}{sinx}+\dfrac{sinx}{1+cosx}\)
\(=\dfrac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+1}{sinx\left(1+cosx\right)}=\dfrac{1}{sinx}\)
Lời giải:
\(E=\cot x+\frac{\sin x}{1+\cos x}=\frac{\cos x}{\sin x}+\frac{\sin x}{1+\cos x}=\frac{\cos x(1+\cos x)+\sin ^2x}{\sin x(\cos x+1)}\)
\(=\frac{\cos x+\sin ^2x+\cos ^2x}{\sin x(\cos x+1)}=\frac{\cos x+1}{\sin x(\cos x+1)}=\frac{1}{\sin x}\)