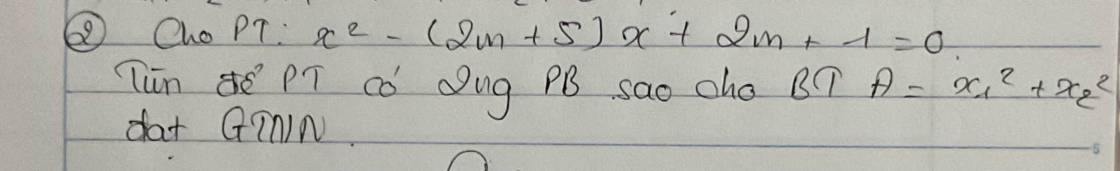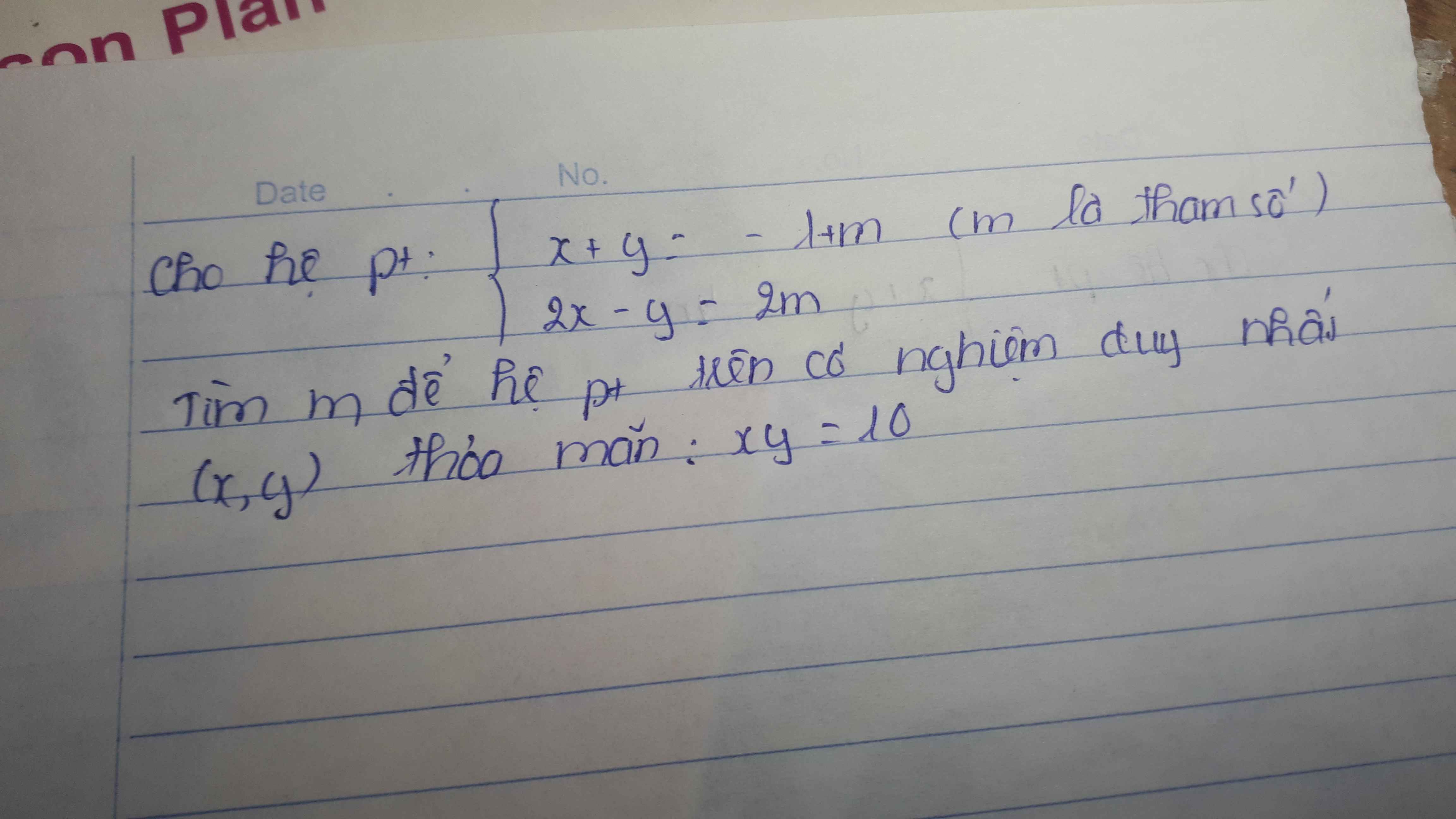\(\Delta=\left(2m+5\right)^2-4\left(2m+1\right)=4m^2+20m+25-8m-4=4m^2+12m+21=4m^2+2.2m.3+9+12=\left(2m+3\right)^2+12>0\)
Vậy pt có 2 nghiệm pb
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m+5\\x_1x_2=2m+1\end{matrix}\right.\)
\(D=\left(x_1+x_2\right)^2-2x_1x_2=\left(2m+5\right)^2-2\left(2m+1\right)\)
\(=4m^2+20m+25-4m-2=4m^2+16m+23=4\left(m^2+4m+4-4\right)+23=4\left(m+2\right)^2+7\ge7\)
Dấu ''='' xảy ra khi m = -2
Đúng 1
Bình luận (1)
