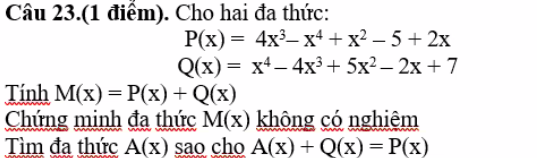`M(x) = P(x) + Q(x)`
`= ( 4x^3 - x^4 + x^2 - 5 + 2x ) + ( x^4 - 4x^3 + 5x^2 - 2x + 7 )`
`= ( 4x^3 - 4x^3 ) + ( x^4 - x^4 ) + ( x^2 + 5x^2 ) + ( 2x-2x ) + ( 7-5 )`
`= 6x^2 + 2`
Do `6x^2 \ge 0 AAx`
`=> 6x^2 + 2 \ge 2 \ne 0`
`=> M(x)` không có nghiệm `.`
`A(x) + Q(x) = P(x)` hay `A(x) = P(x) - Q(x)`
`= ( 4x^3 - x^4 + x^2 - 5 + 2x ) - ( x^4 - 4x^3 + 5x^2 - 2x + 7 )`
`= ( 4x^3 - x^4 + x^2 - 5 + 2x ) - x^4+ 4x^3 - 5x^2 + 2x - 7 `
`= ( 4x^3 + 4x^3 ) + ( -x^4 - x^4 ) + ( x^2 - 5x^2 ) + ( 2x+2x)+(-5-7)`
`= 8x^3 - 2x^4 - 4x^2 + 4x-12`
\(P\left(x\right)=4x^3-x^4+x^2-5+2x\)
\(P\left(x\right)=-x^4+4x^3+x^2+2x-5\)
\(M\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(M\left(x\right)=\left(-x^4+4x^3+x^2+2x-5\right)+\left(x^4-4x^3+5x^2-2x+7\right)\)
\(M\left(x\right)=-x^4+4x^3+x^2+2x-5+x^4-4x^3+5x^2-2x+7\)
\(M\left(x\right)=\left(-x^4+x^4\right)+\left(4x^3-4x^3\right)+\left(x^2+5x^2\right)+\left(2x-2x\right)+\left(-5+7\right)\)
\(M\left(x\right)=6x^2+2\)
\(\text{Đặt M(x)=0}\)
\(\Rightarrow6x^2+2=0\)
\(\Rightarrow6x^2\) \(=0-2=-2\)
\(\Rightarrow x^2\) \(=\left(-2\right):6=\dfrac{-1}{3}\)
\(\Rightarrow x\in\varnothing\)
\(\text{Vậy đa thức M(x) không có nghiệm}\)
\(A\left(x\right)+Q\left(x\right)=P\left(x\right)\)
\(\Rightarrow A\left(x\right)=P\left(x\right)-Q\left(x\right)\)
\(\Rightarrow A\left(x\right)=\left(-x^4+4x^3+x^2+2x-5\right)-\left(x^4-4x^3+5x^2-2x+7\right)\)
\(\Rightarrow A\left(x\right)=-x^4+4x^3+x^2+2x-5-x^4+4x^3-5x^2+2x-7\)
\(\Rightarrow A\left(x\right)=\left(-x^4-x^4\right)+\left(4x^3+4x^3\right)+\left(x^2-5x^2\right)+\left(2x+2x\right)+\left(-5-7\right)\)
\(\Rightarrow A\left(x\right)=-2x^4+8x^3-6x^2+4x-12\)