a: Xét ΔCID vuông tại I và ΔCBA vuông tại B có
góc C chung
=>ΔCID đồng dạng với ΔCBA
b:
CI=CA/2=7,5cm
ΔCID đồng dạng với ΔCBA
=>CI/CB=ID/BA=CD/CA
=>7,5/12=ID/9=CD/15
=>ID/9=5/8=CD/15
=>ID=45/8cm; CD=75/8cm
a: Xét ΔCID vuông tại I và ΔCBA vuông tại B có
góc C chung
=>ΔCID đồng dạng với ΔCBA
b:
CI=CA/2=7,5cm
ΔCID đồng dạng với ΔCBA
=>CI/CB=ID/BA=CD/CA
=>7,5/12=ID/9=CD/15
=>ID/9=5/8=CD/15
=>ID=45/8cm; CD=75/8cm

Giúp mk với ạ, cảm ơn nhìu nha
Bn nào giúp mk với ạ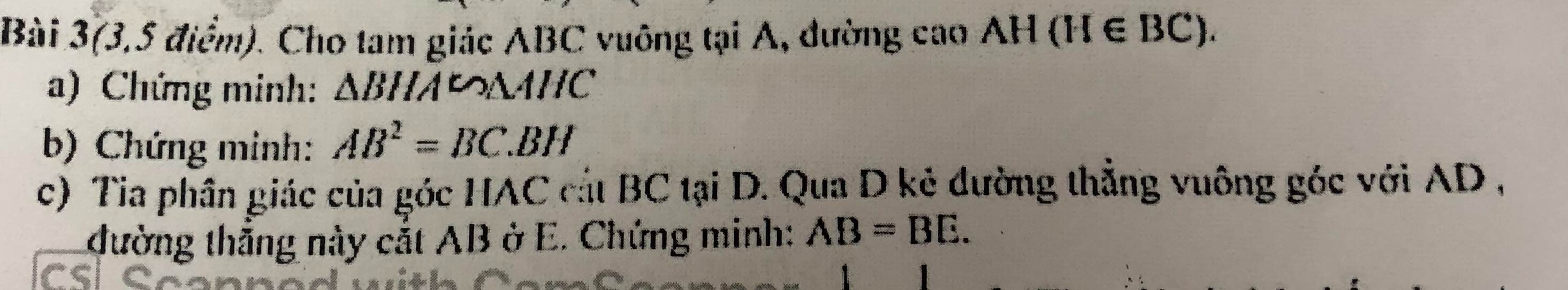
cho tam giác ABC (AB<AC),phân giác AD(D thuộc BC).Gọi H,K lần lượt là hình chiếu của B,C trên AD.
a,CM:tam giác ABH đồng dạng voi tam giác ACK
b,CM: DH.DK=DB.DC
c,CM: AH.CD=AK.BD
d, CM: AH.DK=AK.DH
e. Biết AB=3cm,AC=6cm.Tia CK cat tia AB tại E, tia BH cat AC tại F.CM:SAEC=4SABF
cho tam giác ABC vuông tại A,đường cao AH.
a. CM tam giác ABH đồng dạng với tam giác CBA
b.Gọi E là điểm tùy ý trên cạnh AB, ĐƯờng thẳng đi qua H và vuông góc với HEcawts AC tại F. Tìm vị trí của điểm E trên cạnh AB để tam giác EHFcó diện tích nhỏ nhất
Cho Tam Giác MNP vuông Tại M, đường cao MQ. Cho NQ = 2, NP = 8. Tính MN, MP
Cho tam giác GEF vuông tại G, GH vuông góc với EF, Cho GH = 5, EH = HF. Tính GE
P=\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
1. Tìm giá trị của x để P=\(\dfrac{7}{2}\)
2. Tìm giá trị nhỏ nhất của P
Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là \(54m^2\). Tính độ dài các cạnh của tam giác A'B'C' ?
Giusp vs ạ!
Cho hình bình hành ABCD( AB>BC), điểm M thuộc AB. Đường thẳng DM cắt AC tại K, cắt BC ở N.
a) CMR: tg ADK ~ tg CNK
b) CMR: KM/KD=KA/KC. Từ đó CMR: KD^2 = KM.KN
c) Cho AB=10cm,AD=9cm,AM=6cm. Tính CN và tỉ số diện tích tam giác KCD và tam giác KAM