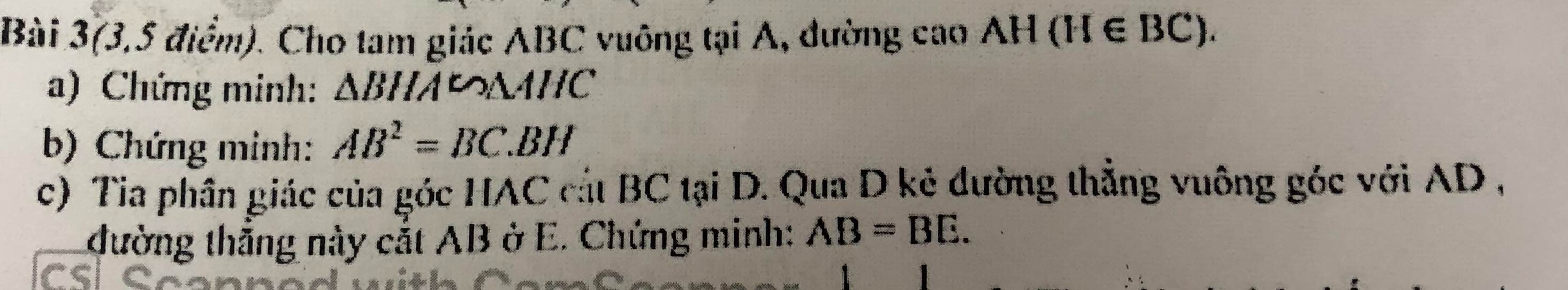a,Xét ΔBAC và ΔAHC có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{BAC}=\widehat{ACH}\) (góc chung)
Vậy ΔBAC\(\sim\)ΔAHC(g−g)
b, Xét ΔABH và ΔCBA có:
\(\widehat{AHB}=\widehat{CAB}=90^o\)
\(\widehat{ABH}=\widehat{CBA}\) (góc chung)
Vậy ΔABH\(\sim\)ΔCBA (g−g)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
\(\Rightarrow\)AB.AB=BC.BH
\(\Rightarrow\)AB2=BC.BH (đpcm)
a,Xét ΔBAC và ΔAHC có:
ˆBAC=ˆAHC=90oBAC^=AHC^=90o
ˆBAC=ˆACHBAC^=ACH^ (góc chung)
Vậy ΔBAC∼∼ΔAHC(g−g)
b, Xét ΔABH và ΔCBA có:
ˆAHB=ˆCAB=90oAHB^=CAB^=90o
ˆABH=ˆCBAABH^=CBA^ (góc chung)
Vậy ΔABH∼∼ΔCBA (g−g)
Cho tam giác vuông góc tại A,đường cao AH, AB=15cm,BC=25cm,BH=9cm a.CM tam giác ABC đồng dạng tam giác HBA và AB.AH=BH.AC b.Phân giác của ^ABC cắt AH tại I, Tính AI và HI c.Phân giác của ^HAC cắt BC tại K. CM IK//AC (có gt kl giups em vs ạ)
