a.
Ta có: \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
b.
\(AH=BH=\dfrac{1}{2}AB=a\) ; \(CH^2=BH^2+BC^2=10a^2\)
\(DH^2=AH^2+AD^2=2a^2\)
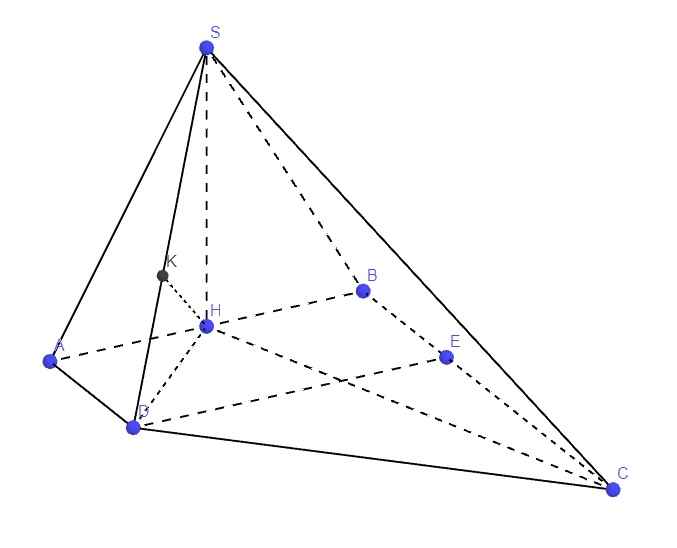
Qua D kẻ đường thẳng song song AB cắt BC tại E
\(\Rightarrow ABED\) là hình chữ nhật \(\Rightarrow BE=AD=a\Rightarrow CE=2a\)
\(\Rightarrow CD^2=DE^2+CE^2=AB^2+CE^2=8a^2\)
\(\Rightarrow CD^2+DH^2=CH^2\Rightarrow\Delta CDH\) vuông tại D
\(\Rightarrow CD\perp DH\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\)
\(\Rightarrow CD\perp\left(SHD\right)\Rightarrow\left(SCD\right)\perp\left(SHD\right)\)
c.
Từ H kẻ \(HK\perp SD\) (K thuộc SD) \(\Rightarrow HK\perp\left(SCD\right)\)
\(\Rightarrow HK=d\left(H;\left(SCD\right)\right)\)
\(SH=\sqrt{SA^2-AH^2}=a\sqrt{3}\)
Hệ thức lượng: \(HK=\dfrac{SH.HD}{\sqrt{SH^2+HD^2}}=\dfrac{a\sqrt{30}}{5}\)
a.
Ta có: {SH⊥(ABCD)⇒SH⊥ADAD⊥AB(gt){SH⊥(ABCD)⇒SH⊥ADAD⊥AB(gt) ⇒AD⊥(SAB)⇒AD⊥(SAB)
b.
HK=SH.HD√SH2+HD2=a√305