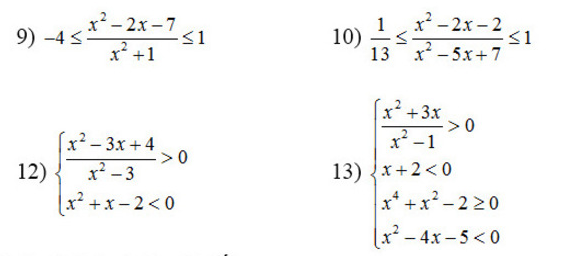a: 1/x-2-1/x<=2/x+2
=>\(\dfrac{x-x+2}{x\left(x-2\right)}-\dfrac{2}{x+2}< =0\)
=>\(\dfrac{1}{x\left(x-2\right)}-\dfrac{1}{x+2}< =0\)
=>\(\dfrac{x+2-x^2+2x}{x\left(x-2\right)\left(x+2\right)}< =0\)
=>\(\dfrac{-x^2+3x+2}{x^3-4x}< =0\)
TH1: -x^2+3x+2>=0 và x^3-4x<0
=>\(\dfrac{3-\sqrt{17}}{2}< =x< =\dfrac{3+\sqrt{17}}{2}\) và (x<-2 hoặc 0<x<2)
=>0<x<2
TH2: -x^2+3x+2<0 và x^3-4x>0
=>(x<(3-căn 17)/2 hoặc x>(3+căn 17)/2) và (-2<x<0 hoặc x>2)
=>x>2 hoặc -2<x<(3-căn 17)/2
b: =>(2x-1)/(x-1)>=2 hoặc (2x-1)/(x-1)<=-2
=>(2x-1-2x+2)/(x-1)>=0 hoặc (2x-1+2x-2)/(x-1)<=0
=>1/(x-1)>=0 hoặc (4x-3)/(x-1)<=0
=>3/4<=x<1 hoặc x>1
c: =>\(\dfrac{x^2-5x+4-x^2+4}{x^2-4}>=0\)
=>(-5x+8)/(x^2-4)>=0
=>(5x-8)/(x^2-4)<=0
TH1: 5x-8>=0 và x^2-4<0
=>-2<x<2 và x>=8/5
=>8/5<=x<2
TH2: 5x-8<0 và x^2-4>0
=>x<8/5 và (x>2 hoặc x<-2)
=>x<-2









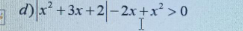 Giải bpt sau :
Giải bpt sau :