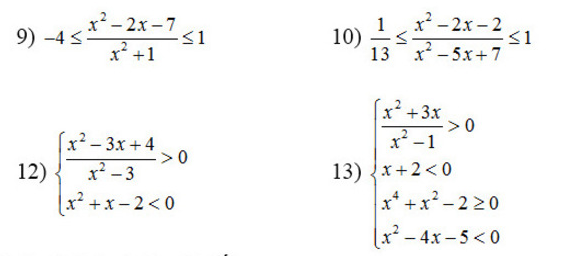1) \(PT\Leftrightarrow\left\{{}\begin{matrix}x^2-4x+3\ge0\\x^2-4x+3>\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le1\\x\ge3\end{matrix}\right.\\x^2-4x+3-x^2+2x-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le1\\x\ge3\end{matrix}\right.\\-2x+2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le1\\x\ge3\end{matrix}\right.\\x< 1\end{matrix}\right.\)
Vậy no của BPT là x<1
2) \(PT\Leftrightarrow\left\{{}\begin{matrix}x+1\ge0\\x+1< \left(x+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x+1-x^2-2x-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\-x^2-x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\\left[{}\begin{matrix}x< -1\\x>0\end{matrix}\right.\end{matrix}\right.\)
Vậy no của BPT là \(x>0\)
Chúc bạn học tốt
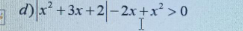Giải bpt sau :
