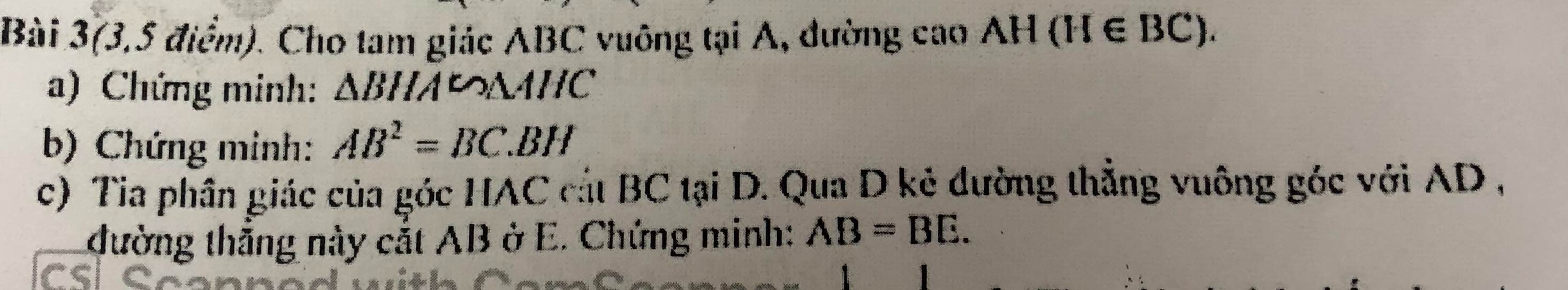a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot10\cdot8=5\cdot8=40\left(cm^2\right)\)
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
c: Xét tứ giác AEHF có \(\widehat{EAF}+\widehat{EHF}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
=>\(\widehat{FEH}=\widehat{FAH}\)
mà \(\widehat{FAH}=\widehat{B}\left(=90^0-\widehat{C}\right)\)
nên \(\widehat{FEH}=\widehat{B}\)
Xét ΔHEF vuông tại H và ΔHBA vuông tại H có
\(\widehat{HEF}=\widehat{HBA}\)
Do đó: ΔHEF đồng dạng với ΔHBA