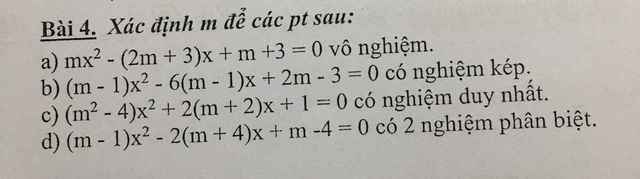a: Trường hợp 1: m=0
Pt sẽ là -3x+3=0
hay x=1
=>Loại
Trường hợp 2: m<>0
\(\Delta=\left(2m+3\right)^2-4m\left(m+3\right)\)
\(=4m^2+12m+9-4m^2-12m\)=9>0
Do đó: Không có giá trị nào của m thỏa mãn
b: Trường hợp 2: m=1
=>Phương trình sẽ là 2-3=0(vô lý)
Trường hợp 2: m<>1
\(\Delta=\left(6m-6\right)^2-4\left(m-1\right)\left(2m-3\right)\)
\(=36m^2-72m+36-4\left(2m^2-3m-2m+3\right)\)
\(=36m^2-72m+36-8m^2+20m-12\)
\(=28m^2-52m+24\)
\(=28m^2-28m-24m+24\)
=(m-1)(28m-24)
Để phương trình có nghiệm kép thì 28m-24=0
hay m=6/7
c: Trường hợp 1: m=2
=>Phương trình sẽ là 8x+1=0
hay x=-1/8(nhận)
Trường hợp 2: m=-2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: \(m\notin\left\{2;-2\right\}\)
\(\Delta=\left(2m+4\right)^2-4\left(m^2-4\right)=4m^2+16m+16-4m^2+16m=32m+16\)
Để phương trình có nghiệm duy nhất thì 32m+16=0
hay m=-1/2