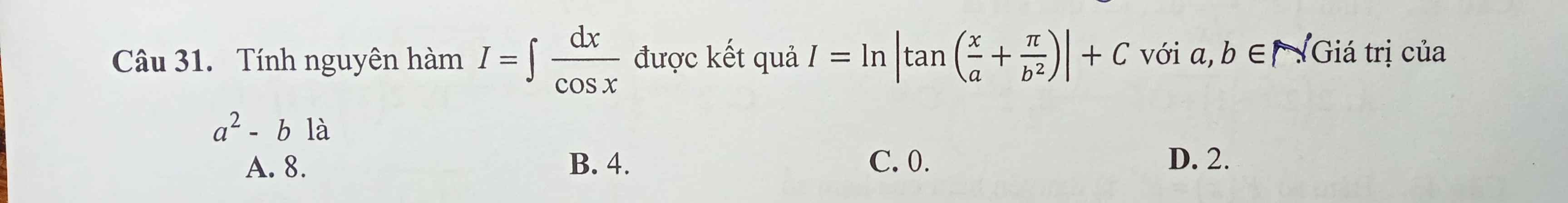\(I=\int\dfrac{dx}{cosx}=\int\dfrac{cosx.dx}{cos^2x}=\int\dfrac{d\left(sinx\right)}{\left(1-sinx\right)\left(1+sinx\right)}\)
\(=\dfrac{1}{2}ln\left|\dfrac{1+sinx}{1-sinx}\right|+C=\dfrac{1}{2}ln\left|\dfrac{\left(1+sinx\right)^2}{cos^2x}\right|+C\)
\(=ln\left|\dfrac{1+sinx}{cosx}\right|+C=ln\left|\dfrac{\left(sin\dfrac{x}{2}+cos\dfrac{x}{2}\right)^2}{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}\right|+C=ln\left|\dfrac{sin\dfrac{x}{2}+cos\dfrac{x}{2}}{cos\dfrac{x}{2}-sin\dfrac{x}{2}}\right|+C\)
\(=ln\left|\dfrac{\sqrt{2}sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}{\sqrt{2}cos\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}\right|+C=ln\left|tan\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)\right|+C\)