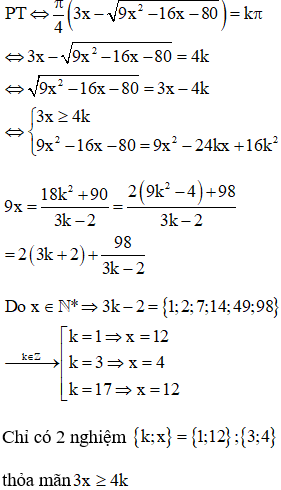ĐKXĐ: \(9x^2-16x-80\ge0\)
\(\Leftrightarrow\dfrac{\pi}{4}\left(3x-\sqrt{9x^2-16x-80}\right)=k\pi\)
\(\Leftrightarrow3x-\sqrt{9x^2-16x-80}=4k\)
\(\Leftrightarrow3x-4k=\sqrt{9x^2-16x-80}\)
\(\Rightarrow9x^2-24kx+16k^2=9x^2-16x-80\)
\(\Rightarrow3kx-2x=2k^2+10\)
\(\Rightarrow x=\dfrac{2k^2+10}{3k-2}>0\Rightarrow k>\dfrac{2}{3}\)
x nguyên dương \(\Rightarrow\dfrac{2k^2+10}{3k-2}\) nguyên dương \(\Rightarrow\dfrac{9\left(2k^2+10\right)}{3k-2}\) nguyên dương
\(\Rightarrow6k+4+\dfrac{98}{3k-2}\) nguyên dương
\(\Rightarrow3k-2=Ư\left(98\right)\) (3k-2 dương nên chỉ cần lấy ước dương)
\(\Rightarrow3k-2=\left\{98;49;14;7;1\right\}\)
\(\Rightarrow k=\left\{17;3;1\right\}\)
Thế vào \(x=\dfrac{2k^2+10}{3k-2}\Rightarrow x=\left\{12;4\right\}\)
.Nhưng khoảng từ pi/2 đến -pi/4 thì vẫn bao gồm đáp án A mà sao mình lại chọn ạ
