a. Trong tam giác vuông ABH ta có:
\(sinA=\dfrac{BH}{AB}\Rightarrow BH=AB.sinA\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BH.AC=\dfrac{1}{2}AB.AC.sinA\) (đpcm)
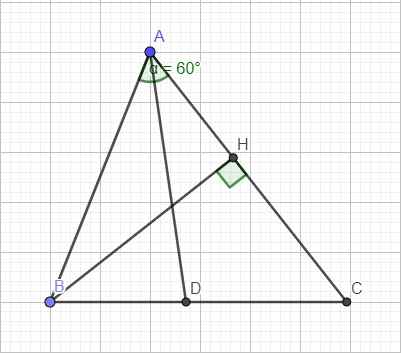
b. Do AD là phân giác nên \(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\widehat{A}=30^0\)
Áp dụng công thức câu a:
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.2.3.sin60^0=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
\(S_{ABD}=\dfrac{1}{2}AB.AD.sin\widehat{BAD}=\dfrac{1}{2}.2.AD.sin30^0=\dfrac{AD}{2}\)
\(S_{ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{1}{2}.3.AD.sin30^0=\dfrac{3AD}{4}\)
Mà \(S_{ABC}=S_{ABD}+S_{ACD}\Rightarrow\dfrac{3\sqrt{3}}{2}=\dfrac{AD}{2}+\dfrac{3AD}{4}\)
\(\Rightarrow AD=\dfrac{6\sqrt{3}}{5}\left(cm\right)\)

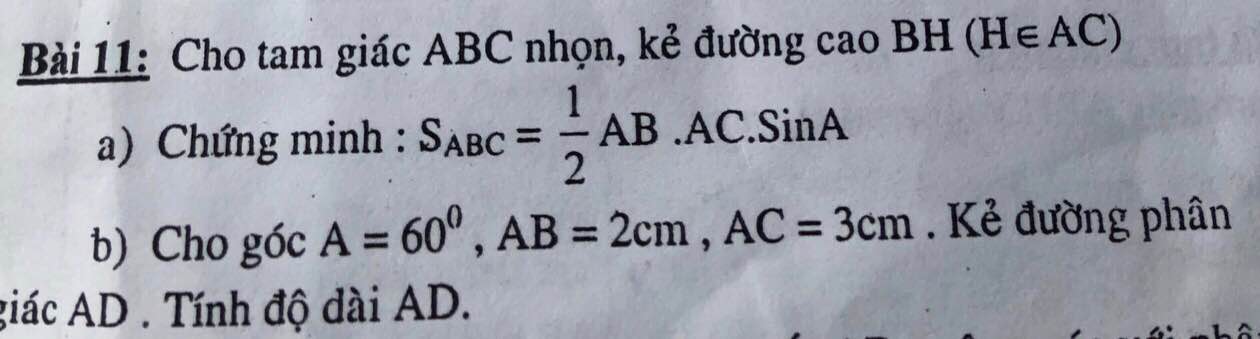







 mong mn giúp em, em cần gấp
mong mn giúp em, em cần gấp





