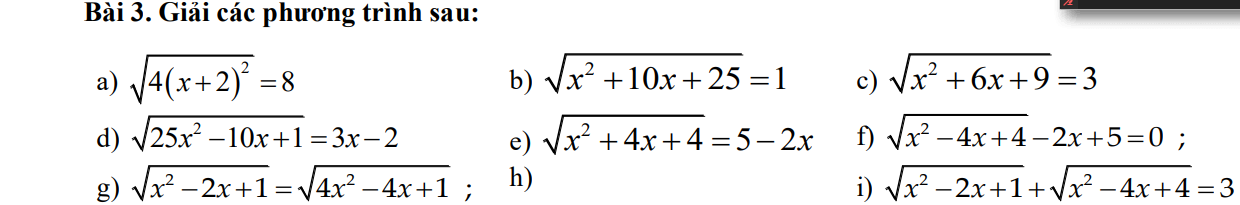a, \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow2\sqrt{\left(x+2\right)^2}=8\)
\(\Leftrightarrow\sqrt{\left(x+2\right)^2}=4\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={2; -6}
b, \(\sqrt{x^2+10x+25}=1\)
\(\Leftrightarrow\sqrt{\left(x+5\right)^2}=1\)
\(\Leftrightarrow\left|x+5\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-6\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={-4;-6}
c, \(\sqrt{x^2+6x+9}=3\)
\(\Leftrightarrow\sqrt{\left(x+3\right)^2}=3\)
\(\Leftrightarrow\left|x+3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=3\\x+3=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={0;-6}
d, \(\sqrt{25x^2-10x+1}=3x-2\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}=3x-2\)
ĐK: \(3x-2\ge0\Leftrightarrow3x\ge2\Leftrightarrow x\ge\dfrac{2}{3}\)
Pt \(\Leftrightarrow\left|5x-1\right|=3x-2\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=3x-2\\5x-1=2-3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-3x=-2+1\\5x+3x=2+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\8x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=\dfrac{3}{8}\end{matrix}\right.\)(cả 2 trường hợp không TM ĐK )
Vậy tập nghiệm của pt là S=\(\varnothing\)
e, \(\sqrt{x^2+4x+4}=5-2x\)
\(\Leftrightarrow\sqrt{\left(x+2\right)^2}=5-2x\)
ĐK: \(5-2x\ge0\Leftrightarrow5\ge2x\Leftrightarrow\dfrac{5}{2}\ge x\) hay \(x\le\dfrac{5}{2}\)
Pt \(\Leftrightarrow\left|x+2\right|=5-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=5-2x\\x+2=2x-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2x=5-2\\2+5=2x-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=3\\x=7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\x=7\left(KTM\right)\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={1}
f, \(\sqrt{x^2-4x+4}-2x+5=0\)
\(\Leftrightarrow\sqrt{x^2-4x+4}=2x-5\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=2x-5\)
ĐK: \(2x-5\ge0\Leftrightarrow2x\ge5\Leftrightarrow x\ge\dfrac{5}{2}\)
Pt \(\Leftrightarrow\left|x-2\right|=2x-5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=2x-5\\x-2=5-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-2+5=2x-x\\x+2x=5+2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\3x=7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(TM\right)\\x=\dfrac{7}{3}\left(KTM\right)\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={3}
g, \(\sqrt{x^2-2x+1}=\sqrt{4x^2-4x+1}\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}=\sqrt{\left(2x-1\right)^2}\)
\(\Leftrightarrow\left|x-1\right|=\left|2x-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=2x-1\\x-1=1-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={0;\(\dfrac{2}{3}\)}
i, \(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=3\)(*)
Bảng xét dấu:
| x | 1 | 2 | |||
| x-1 | - | 0 | + | | | + |
| x-2 | - | | | - | 0 | + |
+ x<1 thì (*)\(\Leftrightarrow1-x+2-x=3\)
\(\Leftrightarrow-2x=0\)
\(\Leftrightarrow x=0\left(TM\right)\)
+1\(\le x\le2\) thì (*)\(\Leftrightarrow x-1+2-x=3\)
\(\Leftrightarrow1=3\)(vô lý)
+x>2 thì (*)\(\Leftrightarrow x-1+x-2=3\)
\(\Leftrightarrow2x-3=3\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=3\left(TM\right)\)
Vậy tập nghiệm của pt là S={0;3}