Mặt phẳng (P): x – 2 = 0 vuông góc với mặt phẳng nào sau đây?
A. (P1): x + 2 = 0. B. (P2): x + y – 2 = 0.
C. (P3): z – 2 = 0. D. (P4): x + z – 2 = 0.
Bài 2: Phương trình đường thẳng
Bài tập 3 (SGK Cánh Diều - Tập 2 - Trang 78)
Thảo luận (1)
Bài tập 2 (SGK Cánh Diều - Tập 2 - Trang 78)
Đường thẳng đi qua điểm B(– 1; 3; 6) nhận overrightarrow{u}left(2;-3;8right) làm vectơ chỉ phương có phương trình chính tắc là:A. dfrac{x-1}{2}dfrac{y+3}{-3}dfrac{z+6}{8} B. dfrac{x+1}{2}dfrac{y-3}{-3}dfrac{z-6}{8}C. dfrac{x+1}{-2}dfrac{y-3}{3}dfrac{z-6}{8} D. dfrac{x+1}{2}dfrac{y-3}{3}dfrac{z-6}{8}
Đọc tiếp
Đường thẳng đi qua điểm B(– 1; 3; 6) nhận \(\overrightarrow{u}=\left(2;-3;8\right)\) làm vectơ chỉ phương có phương trình chính tắc là:
A. \(\dfrac{x-1}{2}=\dfrac{y+3}{-3}=\dfrac{z+6}{8}\) B. \(\dfrac{x+1}{2}=\dfrac{y-3}{-3}=\dfrac{z-6}{8}\)
C. \(\dfrac{x+1}{-2}=\dfrac{y-3}{3}=\dfrac{z-6}{8}\) D. \(\dfrac{x+1}{2}=\dfrac{y-3}{3}=\dfrac{z-6}{8}\)
Thảo luận (1)Hướng dẫn giảiVì đường thẳng đi qua điểm \(B\left( { - 1;3;6} \right)\) nhận \(\overrightarrow u = \left( {2; - 3;8} \right)\) làm vectơ chỉ phương có phương trình chính tắc là: \(\frac{{x - \left( { - 1} \right)}}{2} = \frac{{y - 3}}{{ - 3}} = \frac{{z - 6}}{8} \Leftrightarrow \frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 3}} = \frac{{z - 6}}{8}\)
Chọn B
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 7 (SGK Cánh Diều - Tập 2 - Trang 79)
Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):a) Delta_1:left{{}begin{matrix}x-1+t_1y4+sqrt{3}t_1z0end{matrix}right. và Delta_2:left{{}begin{matrix}x-1+sqrt{3}t_2y4+t_2z5end{matrix}right. (t1, t2 là tham số);b) Delta_1:left{{}begin{matrix}x-1+2ty3+tz4-tend{matrix}right. (t là tham số) và Delta_2:dfrac{x+1}{3}dfrac{y-1}{1}dfrac{z-4}{-2};c) Delta_1:dfrac{x+3}{1}dfrac{y-2}{1}dfrac{z-1}{-1} và Delta_2:dfrac{x+2}{-1}dfrac{y-2}{3}dfrac{z-4}{1}.
Đọc tiếp
Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
a) \(\Delta_1:\left\{{}\begin{matrix}x=-1+t_1\\y=4+\sqrt{3}t_1\\z=0\end{matrix}\right.\) và \(\Delta_2:\left\{{}\begin{matrix}x=-1+\sqrt{3}t_2\\y=4+t_2\\z=5\end{matrix}\right.\) (t1, t2 là tham số);
b) \(\Delta_1:\left\{{}\begin{matrix}x=-1+2t\\y=3+t\\z=4-t\end{matrix}\right.\) (t là tham số) và \(\Delta_2:\dfrac{x+1}{3}=\dfrac{y-1}{1}=\dfrac{z-4}{-2};\)
c) \(\Delta_1:\dfrac{x+3}{1}=\dfrac{y-2}{1}=\dfrac{z-1}{-1}\) và \(\Delta_2:\dfrac{x+2}{-1}=\dfrac{y-2}{3}=\dfrac{z-4}{1}\).
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1;\sqrt 3 ;0} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {\sqrt 3 ;1;0} \right)\).
Ta có: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \frac{{\left| {1.\sqrt 3 + \sqrt 3 .1 + 0.0} \right|}}{{\sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2} + {0^2}} .\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {1^2} + {0^2}} }} = \frac{{\sqrt 3 }}{2}\) nên \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\)
b) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {2;1; - 1} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {3;1; - 2} \right)\).
Ta có: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \frac{{\left| {2.3 + 1.1 + \left( { - 1} \right).\left( { - 2} \right)} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{3^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = \frac{{3\sqrt {21} }}{{14}}\) nên \(\left( {{\Delta _1},{\Delta _2}} \right) \approx {11^o}\)
c) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {1;1; - 1} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( { - 1;3;1} \right)\).
Ta có: \(\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \frac{{\left| {1.\left( { - 1} \right) + 3.1 + 1.\left( { - 1} \right)} \right|}}{{\sqrt {{1^2} + {1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {3^2} + {1^2}} }} = \frac{{\sqrt {33} }}{{33}}\) nên \(\left( {{\Delta _1},{\Delta _2}} \right) \approx {80^o}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 4 (SGK Cánh Diều - Tập 2 - Trang 78)
Cho đường thẳng ∆ có phương trình tham số \(\left\{{}\begin{matrix}x=1-t\\y=3+2t\\z=-1+3t\end{matrix}\right.\) (t là tham số).
a) Chỉ ra tọa độ hai điểm thuộc đường thẳng ∆.
b) Điểm nào trong hai điểm C(6; – 7; – 16), D(– 3; 11; – 11) thuộc đường thẳng ∆?
Thảo luận (1)Hướng dẫn giảia) Với \(t = 0\) ta có: \(\left\{ \begin{array}{l}x = 1 - 0 = 1\\y = 3 + 2.0 = 3\\z = - 1 + 3.0 = - 1\end{array} \right.\) nên điểm \(A\left( {1;3; - 1} \right)\) thuộc đường thẳng \(\Delta \).
Với \(t = 1\) ta có: \(\left\{ \begin{array}{l}x = 1 - 1 = 0\\y = 3 + 2.1 = 5\\z = - 1 + 3.1 = 2\end{array} \right.\) nên điểm \(B\left( {0;5;2} \right)\) thuộc đường thẳng \(\Delta \).
b) Thay \(x = 6;y = - 7;z = - 16\) vào phương trình đường thẳng \(\Delta \) ta có:
\(\left\{ \begin{array}{l}6 = 1 - t\\ - 7 = 3 + 2t\\ - 16 = - 1 + 3t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = - 5\\t = - 5\\t = - 5\end{array} \right. \Leftrightarrow t = - 5\)
Do đó, điểm \(C\left( {6; - 7; - 16} \right)\) thuộc đường thẳng \(\Delta \).
Thay \(x = - 3;y = 11;z = - 11\) vào phương trình đường thẳng \(\Delta \) ta có:
\(\left\{ \begin{array}{l} - 3 = 1 - t\\11 = 3 + 2t\\ - 11 = - 1 + 3t\end{array} \right.\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}t = 4\\t = 4\\t = \frac{{ - 10}}{3}\end{array} \right.\) (vô lí)
Do đó, điểm \(D\left( { - 3;11; - 11} \right)\) không thuộc đường thẳng \(\Delta \).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 6 (SGK Cánh Diều - Tập 2 - Trang 79)
Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:a) Delta_1:dfrac{x-1}{2}dfrac{y-2}{1}dfrac{z-3}{-1} và Delta_2:left{{}begin{matrix}x-11-6ty-6-3tz10+3tend{matrix}right. (t là tham số);b) Delta_2:left{{}begin{matrix}x1+3ty2+4tz3+5tend{matrix}right. (t là tham số) và Delta_2:dfrac{x+3}{1}dfrac{y+6}{2}dfrac{z-15}{-3}.c) Delta_1:dfrac{x+1}{4}dfrac{y-1}{3}dfrac{z}{1} và Delta_2:dfrac{x-1}{1}dfrac{y-3}{2}dfrac{z-1}{2}.
Đọc tiếp
Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:
a) \(\Delta_1:\dfrac{x-1}{2}=\dfrac{y-2}{1}=\dfrac{z-3}{-1}\) và \(\Delta_2:\left\{{}\begin{matrix}x=-11-6t\\y=-6-3t\\z=10+3t\end{matrix}\right.\) (t là tham số);
b) \(\Delta_2:\left\{{}\begin{matrix}x=1+3t\\y=2+4t\\z=3+5t\end{matrix}\right.\) (t là tham số) và \(\Delta_2:\dfrac{x+3}{1}=\dfrac{y+6}{2}=\dfrac{z-15}{-3}\).
c) \(\Delta_1:\dfrac{x+1}{4}=\dfrac{y-1}{3}=\dfrac{z}{1}\) và \(\Delta_2:\dfrac{x-1}{1}=\dfrac{y-3}{2}=\dfrac{z-1}{2}\).
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {2;1; - 1} \right)\) và đi qua điểm \(A\left( {1;2;3} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( { - 6; - 3;3} \right)\) và đi qua điểm \(B\left( { - 11; - 6;10} \right)\).
Vì \( - 3\overrightarrow {{u_1}} = \left( { - 6; - 3;3} \right) = \overrightarrow {{u_2}} \), suy ra \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương.
Lại có: \(\overrightarrow {AB} = \left( { - 12; - 8;7} \right)\) và \(\frac{2}{{ - 12}} \ne \frac{1}{{ - 8}}\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{M_1}{M_2}} \) không cùng phương.
Vậy \({\Delta _1}//{\Delta _2}\).
b) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {3;4;5} \right)\) và đi qua điểm \(A\left( {1;2;3} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;2; - 3} \right)\) và đi qua điểm \(B\left( { - 3; - 6;15} \right)\).
Ta có: \(\frac{3}{1} \ne \frac{4}{2}\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.
Lại có: \(\overrightarrow {AB} = \left( { - 4; - 8;12} \right)\), \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}4&5\\2&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&3\\{ - 3}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&4\\1&2\end{array}} \right|} \right) = \left( { - 22;14;2} \right)\)
Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {AB} = \left( { - 22} \right).\left( { - 4} \right) + 14.\left( { - 8} \right) + 2.12 = 0\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ,\overrightarrow {AB} \) đồng phẳng. Vậy \({\Delta _1}\) cắt \({\Delta _2}\).
c) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {4;3;1} \right)\) và đi qua điểm \(A\left( { - 1;1;0} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;2;2} \right)\) và đi qua điểm \(B\left( {1;3;1} \right)\).
Ta có: \(\frac{4}{1} \ne \frac{3}{2}\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.
Lại có: \(\overrightarrow {AB} = \left( {2;2;1} \right)\), \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}3&1\\2&2\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&4\\2&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}4&3\\1&2\end{array}} \right|} \right) = \left( {4; - 7;5} \right)\)
Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {AB} = 4.2 - 7.2 + 5.1 = - 1 \ne 0\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ,\overrightarrow {AB} \) không đồng phẳng. Vậy \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 8 (SGK Cánh Diều - Tập 2 - Trang 79)
Tính góc giữa đường thẳng ∆ và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):a) Delta:left{{}begin{matrix}x1+sqrt{3}ty2z3+tend{matrix}right. (t là tham số) và (P): sqrt{3}x+z-20;b) Delta:left{{}begin{matrix}x1+ty2-tz3+tend{matrix}right. (t là tham số) và (P): x + y + z - 4 0.
Đọc tiếp
Tính góc giữa đường thẳng ∆ và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
a) \(\Delta:\left\{{}\begin{matrix}x=1+\sqrt{3}t\\y=2\\z=3+t\end{matrix}\right.\) (t là tham số) và (P): \(\sqrt{3}x+z-2=0\);
b) \(\Delta:\left\{{}\begin{matrix}x=1+t\\y=2-t\\z=3+t\end{matrix}\right.\) (t là tham số) và (P): x + y + z - 4 = 0.
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \(\Delta \) có một vectơ chỉ phương \(\overrightarrow u = \left( {\sqrt 3 ;0;1} \right)\).
Mặt phẳng (P) có một vectơ pháp tuyến \(\overrightarrow n = \left( {\sqrt 3 ;0;1} \right)\).
Ta có: \(\sin \left( {\left( P \right),\Delta } \right) = \frac{{\left| {\sqrt 3 .\sqrt 3 + 0.0 + 1.1} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {0^2} + {1^2}} .\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {0^2} + {1^2}} }} = \frac{4}{4} = 1\) nên \(\left( {\left( P \right),\Delta } \right) = {90^o}\).
b) Đường thẳng \(\Delta \) có một vectơ chỉ phương \(\overrightarrow u = \left( {1; - 1;1} \right)\).
Mặt phẳng (P) có một vectơ pháp tuyến \(\overrightarrow n = \left( {1;1;1} \right)\).
Ta có: \(\sin \left( {\left( P \right),\Delta } \right) = \frac{{\left| {1.1 + \left( { - 1} \right).1 + 1.1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} .\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{1}{3}\) nên \(\left( {\left( P \right),\Delta } \right) \approx {19^o}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 10 (SGK Cánh Diều - Tập 2 - Trang 80)
Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp S.ABCD có các đỉnh lần lượt là Sleft(0;0;dfrac{asqrt{3}}{2}right),Aleft(dfrac{a}{2};0;0right),Bleft(-dfrac{a}{2};0;0right),Cleft(-dfrac{a}{2};a;0right),Dleft(dfrac{a}{2};a;0right) với a 0 (Hình 36).a) Xác định tọa độ của các vectơ overrightarrow{SA},overrightarrow{CD}. Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).b) Chỉ ra một vectơ pháp tuyến của mặt phẳng (SAC). Từ đó tính góc giữa đường thẳng SD...
Đọc tiếp
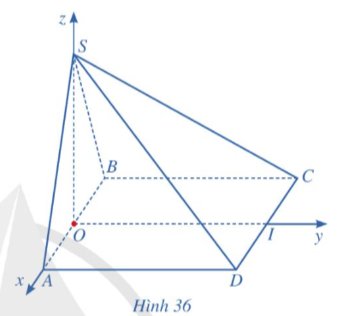
Trong không gian với hệ trục tọa độ Oxyz, cho hình chóp S.ABCD có các đỉnh lần lượt là \(S\left(0;0;\dfrac{a\sqrt{3}}{2}\right),A\left(\dfrac{a}{2};0;0\right),B\left(-\dfrac{a}{2};0;0\right),C\left(-\dfrac{a}{2};a;0\right),D\left(\dfrac{a}{2};a;0\right)\) với a > 0 (Hình 36).
a) Xác định tọa độ của các vectơ \(\overrightarrow{SA},\overrightarrow{CD}\). Từ đó tính góc giữa hai đường thẳng SA và CD (làm tròn kết quả đến hàng đơn vị của độ).
b) Chỉ ra một vectơ pháp tuyến của mặt phẳng (SAC). Từ đó tính góc giữa đường thẳng SD và mặt phẳng (SAC) (làm tròn kết quả đến hàng đơn vị của độ).
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {SA} = \left( {\frac{a}{2};0;\frac{{ - a\sqrt 3 }}{2}} \right),\overrightarrow {CD} = \left( {a;0;0} \right)\).
Do đó, \(\cos \left( {SA,CD} \right) = \frac{{\left| {\frac{a}{2}.a + 0.0 - \frac{{a\sqrt 3 }}{2}.0} \right|}}{{\sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {0^2} + {{\left( {\frac{{ - a\sqrt 3 }}{2}} \right)}^2}} .\sqrt {{a^2} + {0^2} + {0^2}} }} = \frac{1}{2}\) nên \(\left( {SA,CD} \right) = {60^o}\).
b) Mặt phẳng (SAC) nhận \(\left[ {\overrightarrow {SA} ,\overrightarrow {AC} } \right]\) làm một vectơ pháp tuyến.
Ta có: \(\overrightarrow {SA} = \left( {\frac{a}{2};0;\frac{{ - a\sqrt 3 }}{2}} \right),\overrightarrow {AC} = \left( { - a;a;0} \right),\overrightarrow {SD} = \left( {\frac{a}{2};a;\frac{{ - a\sqrt 3 }}{2}} \right)\).
\(\left[ {\overrightarrow {SA} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{\frac{{ - a\sqrt 3 }}{2}}\\a&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\frac{{ - a\sqrt 3 }}{2}}&{\frac{a}{2}}\\0&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\frac{a}{2}}&0\\{ - a}&a\end{array}} \right|} \right) = \left( {\frac{{{a^2}\sqrt 3 }}{2};\frac{{{a^2}\sqrt 3 }}{2};\frac{{{a^2}}}{2}} \right)\)
Do đó, \(\sin \left( {\left( {SAC} \right),SD} \right) = \frac{{\left| {\frac{{{a^2}\sqrt 3 }}{2}.\frac{a}{2} + \frac{{{a^2}\sqrt 3 }}{2}.a + \frac{{{a^2}}}{2}.\frac{{ - a\sqrt 3 }}{2}} \right|}}{{\sqrt {{{\left( {\frac{{{a^2}\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{{a^2}\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{{a^2}}}{2}} \right)}^2}} \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {a^2} + {{\left( {\frac{{ - a\sqrt 3 }}{2}} \right)}^2}} }} = \frac{{\sqrt {42} }}{{14}}\).
Suy ra, \(\left( {\left( {SAC} \right),SD} \right) \approx {28^o}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 11 (SGK Cánh Diều - Tập 2 - Trang 80)
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).a) Viết phương trình đường thẳng AB.b) Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy)) có nằm trong phạm vi cho phép từ 2,5° đến 3,5° hay không.c) Có một lớp mây được mô phỏng bởi một mặt phẳng (α) đi qua ba điểm M(5; 0; 0), N(0; – 5; 0), P(0; 0; 0,5). Tìm tọa độ của điểm C là vị trí...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí A(3,5; – 2; 0,4) và sẽ hạ cánh ở vị trí B(3,5; 5,5; 0) trên đường băng EG (Hình 37).
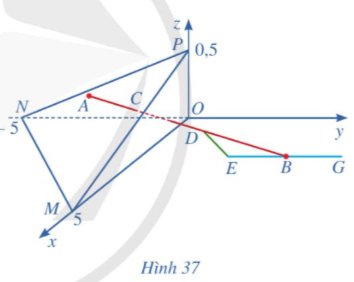
a) Viết phương trình đường thẳng AB.
b) Hãy cho biết góc trượt (góc giữa đường bay AB và mặt phẳng nằm ngang (Oxy)) có nằm trong phạm vi cho phép từ 2,5° đến 3,5° hay không.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng (α) đi qua ba điểm M(5; 0; 0), N(0; – 5; 0), P(0; 0; 0,5). Tìm tọa độ của điểm C là vị trí mà máy bay xuyên qua đám mây để hạ cánh.
d) Tìm tọa độ của điểm D trên đoạn thẳng AB là vị trí mà máy bay ở độ cao 120 m.
e) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu E(3,5; 4,5; 0) của đường băng ở độ cao tối thiểu là 120 m. Hỏi sau khi ra khỏi đám mây, người phi công có đạt được quy định an toàn đó hay không? Biết rằng tầm nhìn của người phi công sau khi ra khỏi đám mây là 900 m (Nguồn: R.Larson and B.Edwards, Calculus 10e, Cengage, 2014).
Thảo luận (1)Hướng dẫn giảia) Đường thẳng AB đi qua điểm \(A\left( {3,5; - 2;0,4} \right)\) và nhận \(\overrightarrow {AB} = \left( {0;7,5; - 0,4} \right)\) làm một vectơ chỉ phương nên phương trình tham số của đường thẳng AB là:
\(\left\{ \begin{array}{l}x = 3,5\\y = - 2 + 7,5t\\z = 0,4 - 0,4t\end{array} \right.\) (t là tham số).
b) Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\).
Do đó, \(\sin \left( {AB,\left( {Oxy} \right)} \right) = \frac{{\left| {0.0 + 7,5.0 + \left( { - 0,4} \right).1} \right|}}{{\sqrt {{0^2} + {{\left( { - 7,5} \right)}^2} + {{\left( { - 0,4} \right)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{4\sqrt {5641} }}{{5641}}\) nên \(\left( {AB,\left( {Oxy} \right)} \right) \approx {3^o}\). Do đó, góc trượt nằm trong phạm vi cho phép.
c) Mặt phẳng \(\left( \alpha \right)\) là mặt phẳng (MNP).
Ta có: \(\overrightarrow {MN} = \left( { - 5; - 5;0} \right),\overrightarrow {MP} = \left( { - 5;0;0,5} \right)\)
Ta có: \(\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 5}&0\\0&{0,5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 5}\\{0,5}&{ - 5}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 5}&{ - 5}\\{ - 5}&0\end{array}} \right|} \right) = \left( { - 2,5;2,5; - 25} \right)\)
Mặt phẳng (MNP) nhận \(\left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( { - 2,5;2,5; - 25} \right)\) làm một vectơ pháp tuyến.
Do đó, phương trình mặt phẳng \(\left( \alpha \right)\) là:
\( - 2,5\left( {x - 5} \right) + 2,5\left( {y - 0} \right) - 25\left( {z - 0} \right) \Leftrightarrow x - y + 10z - 5 = 0\)
Vì C là vị trí mà máy bay xuyên qua đám mấy để hạ cánh nên C là giao điểm của đường thẳng AB và mặt phẳng \(\left( \alpha \right)\).
Vì C thuộc AB nên \(C\left( {3,5; - 2 + 7,5t;0,4 - 0,4t} \right)\). Mà C thuộc mặt phẳng \(\left( \alpha \right)\) nên:
\(3,5 - \left( { - 2 + 7,5t} \right) + 10\left( {0,4 - 0,4t} \right) - 5 = 0\), suy ra \(t = \frac{9}{{23}}\). Do đó, \(C\left( {\frac{7}{2};\frac{{43}}{{46}};\frac{{28}}{{115}}} \right)\).
d) Vì D thuộc AB nên \(D\left( {3,5; - 2 + 7,5t';0,4 - 0,4t'} \right)\)
D là vị trí mà máy bay ở độ cao 120m, tức là khoảng cách từ D đến mặt phẳng (Oxy) bằng 120m và bằng 0,12km.
Ta có: \(d\left( {D,\left( {Oxy} \right)} \right) = \frac{{\left| {0,4 - 0,4t'} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = \left| {0,4 - 0,4t'} \right|\)
Do đó, \(\left| {0,4 - 0,4t'} \right| = 0,12 \Leftrightarrow \left[ \begin{array}{l}0,4 - 0,4t' = 0,12\\0,4 - 0,4t' = - 0,12\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t' = 0,7\\t' = 1,3\end{array} \right.\)
Với \(t' = 0,7\) ta có \(D\left( {3,5;3,25;0,12} \right)\).
Với \(t' = 1,3\) ta có \(D\left( {3,5;7,75; - 0,12} \right)\).
Vì D là vị trí độ cao của máy bay nên \(D\left( {3,5;3,25;0,12} \right)\).
e) Ta có: \(DE = \sqrt {{{\left( {3,5 - 3,5} \right)}^2} + {{\left( {4,5 - 3,25} \right)}^2} + {{\left( {0 - 0,12} \right)}^2}} \approx 1,256\left( {km} \right)\)
Vì tầm nhìn xa của phi công sau khi ra khỏi đám mây là \(900m = 0,9km < 1,256km\) nên người phi công đó không đạt được quy định an toàn bay.
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 9 (SGK Cánh Diều - Tập 2 - Trang 79)
Tính góc giữa hai mặt phẳng (P1): x + y + 2z – 1 = 0 và (P2): 2x – y + z – 2 = 0.
Thảo luận (1)Hướng dẫn giảiMặt phẳng \(\left( {{P_1}} \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {1;1;2} \right)\); mặt phẳng \(\left( {{P_2}} \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {2; - 1;1} \right)\).
Do đó, \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {1.2 + 1\left( { - 1} \right) + 2.1} \right|}}{{\sqrt {{1^2} + {1^2} + {2^2}} \sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{1}{2}\) nên \(\left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = {60^o}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5 (SGK Cánh Diều - Tập 2 - Trang 78)
Viết phương trình tham số và phương trình chính tắc của đường thẳng ∆ trong mỗi trường hợp sau:
a) ∆ đi qua điểm A(– 1; 3; 2) và có vectơ chỉ phương \(\overrightarrow{u}=\left(-2;3;4\right)\);
b) ∆ đi qua điểm M(2; – 1; 3) và N(3; 0; 4).
Thảo luận (1)Hướng dẫn giảia) Vì đường \(\Delta \) đi qua điểm \(A\left( { - 1;3;2} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 2;3;4} \right)\) nên:
+ Phương trình tham số: \(\left\{ \begin{array}{l}x = - 1 - 2t\\y = 3 + 3t\\z = 2 + 4t\end{array} \right.\) (t là tham số).
+ Phương trình chính tắc: \(\frac{{x + 1}}{{ - 2}} = \frac{{y - 3}}{3} = \frac{{z - 2}}{4}\).
b) Vì \(\Delta \) đi qua hai điểm \(M\left( {2; - 1;3} \right)\) và \(N\left( {3;0;4} \right)\) nên phương trình chính tắc của \(\Delta \) là:
\(\frac{{x - 2}}{{3 - 2}} = \frac{{y + 1}}{{0 + 1}} = \frac{{z - 3}}{{4 - 3}} \Leftrightarrow \frac{{x - 2}}{1} = \frac{{y + 1}}{1} = \frac{{z - 3}}{1}\).
Phương trình tham số của \(\Delta \): \(\left\{ \begin{array}{l}x = 2 + t\\y = - 1 + t\\z = 3 + t\end{array} \right.\) (t là tham số).
(Trả lời bởi Nguyễn Quốc Đạt)