Cầu Bãi Cháy nối Hòn Gai và Bãi Cháy (Quảng Ninh). Dây cáp của cầu gợi nên hình ảnh đường thẳng trong không gian với hệ tọa độ Oxyz (Hình 22).
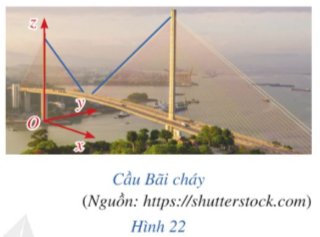
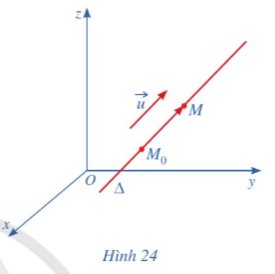
Trong hệ tọa độ Oxyz, phương trình của đường thẳng là gì? Làm thế nào để lập được phương trình của đường thẳng?
Cho hình hộp ABCD.A'B'C'D' (Hình 23). Giá của vectơ \(\overrightarrow{A'C'}\) và đường thẳng AC có vị trí tương đối như thế nào?
Thảo luận (1)Hướng dẫn giảiGiá của vectơ \(\overrightarrow {A'C'} \) là đường thẳng A’C’. Mà AC//A’C’ (do ABCD.A’B’C’D’ là hình hộp) nên giá của vectơ \(\overrightarrow {A'C'} \) song song đường thẳng AC.
(Trả lời bởi Nguyễn Quốc Đạt)
Trong Hình 23, vectơ \(\overrightarrow{B'D'}\) có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?
Thảo luận (1)Hướng dẫn giảiGiá của vectơ \(\overrightarrow {B'D'} \) là đường thẳng B’D’. Mà BD//B’D’ (do ABCD.A’B’C’D’ là hình hộp) nên vectơ \(\overrightarrow {B'D'} \) là vectơ chỉ phương của đường thẳng BD.
(Trả lời bởi Nguyễn Quốc Đạt)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M0(1; 2; 3) và có vectơ chỉ phương \(\overrightarrow{u}=\left(2;3;5\right)\). Xét điểm M(x; y; z) nằm trên ∆ (Hình 24).
a) Nêu nhận xét về phương của hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{M_0M}\).
b) Có hay không số thực t sao cho \(\overrightarrow{M_0M}=t\overrightarrow{u}\)?
c) Hãy biểu diễn x, y, z qua t.
d) Tọa độ (x; y; z) của điểm M (nằm trên ∆) có thỏa mãn hệ phương trình:
\(\left\{{}\begin{matrix}x=1+2t\\y=2+3t\\z=3+5t\end{matrix}\right.\) (t là tham số).
Thảo luận (1)Hướng dẫn giảia) Hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau.
b) Vì hai vectơ \(\overrightarrow u \) và \(\overrightarrow {{M_o}M} \) cùng phương với nhau nên tồn tại số thực t khác 0 sao cho \(\overrightarrow {{M_o}M} = t\overrightarrow u \).
c) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - 1;y - 2;z - 3} \right)\).
Theo b ta có: \(\overrightarrow {{M_o}M} = t\overrightarrow u \) nên \(\left\{ \begin{array}{l}x - 1 = 2t\\y - 2 = - 3t\\z - 3 = 5t\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = 2t + 1\\y = - 3t + 2\\z = 5t + 3\end{array} \right.\).
d) Vì \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) và theo b ta có \(\left\{ \begin{array}{l}x = 2t + 1\\y = - 3t + 2\\z = 5t + 3\end{array} \right.\) nên tọa độ (x; y; z) của điểm M (nằm trên \(\Delta \)) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 3t\\z = 3 + 5t\end{array} \right.\).
(Trả lời bởi Nguyễn Quốc Đạt)
Viết phương trình tham số của đường thẳng ∆, biết ∆ đi qua điểm C(1; 2; – 4) và vuông góc với mặt phẳng (P):
3x – y + 2z – 1 = 0.
Thảo luận (1)Hướng dẫn giảiMặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n \left( {3; - 1;2} \right)\).
Vì đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) nên đường thẳng \(\Delta \) nhận \(\overrightarrow n \left( {3; - 1;2} \right)\) làm một vectơ chỉ phương.
Lại có, \(\Delta \) đi qua điểm \(C\left( {1;2; - 4} \right)\) nên phương trình tham số của đường thẳng \(\Delta \) là: \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 - t\\z = - 4 + 2t\end{array} \right.\) (t là tham số).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường thẳng ∆ có phương trình tham số:
\(\left\{{}\begin{matrix}x=2+3t\\y=4+7t\\z=5+8t\end{matrix}\right.\) (t là tham số).
Tọa độ (x; y; z) của điểm M (nằm trên ∆) có thỏa mãn hệ phương trình \(\dfrac{x-2}{3}=\dfrac{y-4}{7}=\dfrac{z-5}{8}\) hay không?
Thảo luận (1)Hướng dẫn giảiVì M (x; y; z) nằm trên \(\Delta \) nên \(\left\{ \begin{array}{l}x = 2 + 3t\\y = 4 + 7t\\z = 5 + 8t\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}t = \frac{{x - 2}}{3}\\t = \frac{{y - 4}}{7}\\t = \frac{{z - 5}}{8}\end{array} \right.\). Do đó, \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\).
Do đó, điểm M(x; y; z) nằm trên \(\Delta \) thỏa mãn hệ phương trình \(\frac{{x - 2}}{3} = \frac{{y - 4}}{7} = \frac{{z - 5}}{8}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Viết phương trình chính tắc của đường thẳng ∆, biết phương trình tham số của ∆ là: \(\left\{{}\begin{matrix}x=-1+2t\\y=3-5t\\z=6+9t\end{matrix}\right.\) (t là tham số).
Thảo luận (1)Hướng dẫn giảiĐường thẳng \(\Delta \) đi qua \(M\left( { - 1;3;6} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 5;9} \right)\) nên phương trình chính tắc của đường thẳng \(\Delta \) là: \(\frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z - 6}}{9}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 2; 3) và B(3; 5; 9).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng AB.
b) Viết phương trình tham số của đường thẳng AB.
c) Viết phương trình chính tắc của đường thẳng AB.
Thảo luận (1)Hướng dẫn giảia) Một vectơ chỉ phương của đường thẳng AB là \(\overrightarrow {AB} = \left( {2;3;6} \right)\).
b) Đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;6} \right)\).
Mà đường thẳng AB đi qua điểm \(A\left( {1;2;3} \right)\) nên phương trình tham số của đường thẳng AB là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + 3t\\z = 3 + 6t\end{array} \right.\) (t là tham số).
c) Phương trình chính tắc của đường thẳng AB là: \(\frac{{x - 1}}{2} = \frac{{y - 2}}{3} = \frac{{z - 3}}{6}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Viết phương trình chính tắc của đường thẳng OM, biết M(a; b; c) với abc ≠ 0.
Thảo luận (1)Hướng dẫn giảiPhương trình chính tắc của đường thẳng OM là: \(\frac{{x - 0}}{a} = \frac{{y - 0}}{b} = \frac{{z - 0}}{c} \Leftrightarrow \frac{x}{a} = \frac{y}{b} = \frac{z}{c}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai đường thẳng phân biệt ∆1, ∆2 lần lượt đi qua các điểm M1, M2 và tương ứng có vectơ chỉ phương là \(\overrightarrow{u_1},\overrightarrow{u_2}\).
a) Giả sử ∆1 song song với ∆2 (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow{u_1}\) và \(\overrightarrow{u_2}\); \(\overrightarrow{u_1}\) và \(\overrightarrow{M_1M_2}\)?
b) Giả sử ∆1 và ∆2 cắt nhau (Hình 26). Hai vectơ \(\overrightarrow{u_1}\) và \(\overrightarrow{u_2}\) có cùng phương hay không? Ba vectơ \(\overrightarrow{u_1},\overrightarrow{u_2}\) và \(\overrightarrow{M_1M_2}\) có đồng phẳng hay không?
c) Giả sử ∆1 và ∆2 chéo nhau (Hình 27). Hai vectơ \(\overrightarrow{u_1}\) và \(\overrightarrow{u_2}\) có cùng phương hay không? Ba vectơ \(\overrightarrow{u_1},\overrightarrow{u_2}\) và \(\overrightarrow{M_1M_2}\) có đồng phẳng hay không?
Thảo luận (1)Hướng dẫn giảia) Vì \({\Delta _1}\) song song với \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương.
Vì \({M_1}\) thuộc đường thẳng \({\Delta _1}\), \({M_2}\) thuộc đường thẳng \({\Delta _2}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \) không cùng phương.
b) Vì \({\Delta _1}\) và \({\Delta _2}\) cắt nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) đồng phẳng.
c) Vì \({\Delta _1}\) và \({\Delta _2}\) chéo nhau nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương. Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) không đồng phẳng.
(Trả lời bởi Nguyễn Quốc Đạt)