Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng \(\Delta_1:\left\{{}\begin{matrix}x=t_1\\y=1\\z=0\end{matrix}\right.\) và \(\Delta_2:\left\{{}\begin{matrix}x=2\\y=t_2\\z=0\end{matrix}\right.\) (t1, t2 là tham số).
Bài 2: Phương trình đường thẳng
Luyện tập 5 (SGK Cánh Diều - Tập 2 - Trang 70)
Thảo luận (1)
Hoạt động 6 (SGK Cánh Diều - Tập 2 - Trang 71)
Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là overrightarrow{u_1},overrightarrow{u_2}. Giả sử ∆1, ∆2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).a) Nếu mối liên hệ giữa hai góc (∆1, ∆2) và (∆1, ∆2).b) Gọi A và B là các điểm lần lượt thuộc hai đường thẳng ∆1 và ∆2 sao cho overrightarrow{IA}overrightarrow{u_1},overrightarrow{IB}overrightarrow{u_2}. So sánh: cosleft(Delta_1,Delta_2right),left|cosleft(overrightarrow{IA},...
Đọc tiếp
Cho hai đường thẳng ∆1, ∆2 trong không gian có vectơ chỉ phương lần lượt là \(\overrightarrow{u_1},\overrightarrow{u_2}\). Giả sử ∆'1, ∆'2 là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với ∆1, ∆2 (Hình 28).
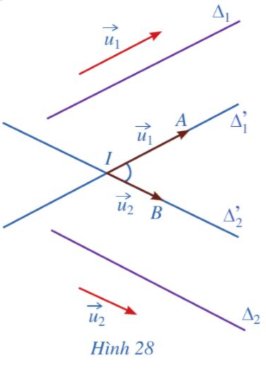
a) Nếu mối liên hệ giữa hai góc (∆1, ∆2) và (∆'1, ∆'2).
b) Gọi A và B là các điểm lần lượt thuộc hai đường thẳng ∆'1 và ∆'2 sao cho \(\overrightarrow{IA}=\overrightarrow{u_1},\overrightarrow{IB}=\overrightarrow{u_2}\). So sánh:
\(\cos\left(\Delta'_1,\Delta'_2\right),\left|\cos\left(\overrightarrow{IA},\overrightarrow{IB}\right)\right|,\left|\cos\left(\overrightarrow{u_1},\overrightarrow{u_2}\right)\right|\).
c) So sánh \(\cos\left(\Delta_1,\Delta_2\right)\) và \(\dfrac{\left|\overrightarrow{u_1}.\overrightarrow{u_2}\right|}{\left|\overrightarrow{u_1}\right|.\left|\overrightarrow{u_2}\right|}\).
Thảo luận (1)Hướng dẫn giảia) Vẽ hai đường thẳng \(\Delta _1',\Delta _2'\) cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\).
b) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) và \(\Delta _1'\) song song (hoặc trùng) với \({\Delta _1}\) nên \(\Delta _1' \bot \left( {{P_1}} \right)\).
Tương tự ta có: \(\Delta _2' \bot \left( {{P_2}} \right)\).
Khi đó, góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\) luôn là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) nên góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) không phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 6 (SGK Cánh Diều - Tập 2 - Trang 72)
Cho đường thẳng \(\Delta:\dfrac{x}{2}=\dfrac{y}{-1}=\dfrac{z}{2}\). Tính côsin của góc giữa đường thẳng ∆ và các trục tọa độ.
Hoạt động 7 (SGK Cánh Diều - Tập 2 - Trang 73)
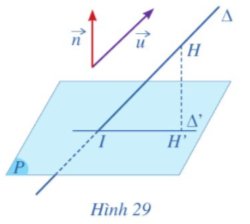
Cho mặt phẳng (P) có vectơ pháp tuyến là overrightarrow{n}, đường thẳng ∆ có vectơ chỉ phương là overrightarrow{u} và đường thẳng ∆ cắt mặt phẳng (P) tại I. Gọi ∆ là hình chiếu của ∆ trên mặt phẳng (P) (Hình 29).a) Hãy xác định góc giữa đường thẳng ∆ và mặt phẳng (P).Ta kí hiệu góc đó là (∆, (P)).b) So sánh sin (∆, (P)) và left|cosleft(overrightarrow{u},overrightarrow{n}right)right|.
Đọc tiếp
Cho mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow{n}\), đường thẳng ∆ có vectơ chỉ phương là \(\overrightarrow{u}\) và đường thẳng ∆ cắt mặt phẳng (P) tại I. Gọi ∆' là hình chiếu của ∆ trên mặt phẳng (P) (Hình 29).
a) Hãy xác định góc giữa đường thẳng ∆ và mặt phẳng (P).
Ta kí hiệu góc đó là (∆, (P)).
b) So sánh sin (∆, (P)) và \(\left|\cos\left(\overrightarrow{u},\overrightarrow{n}\right)\right|\).
Luyện tập 7 (SGK Cánh Diều - Tập 2 - Trang 73)
Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow{n}=\left(A;B;C\right)\). Tính sin của góc giữa mặt phẳng (P) và các trục tọa độ.
Hoạt động 8 (SGK Cánh Diều - Tập 2 - Trang 74)
Cho hai mặt phẳng (P1) và (P2). Lấy hai đường thẳng ∆1, ∆2 sao cho ∆1 ⊥ (P1), ∆2 ⊥ (P2) (Hình 31).a) Nêu cách xác định góc giữa hai đường thẳng ∆1, ∆2.b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng ∆1, ∆2 như trên hay không?
Đọc tiếp
Cho hai mặt phẳng (P1) và (P2). Lấy hai đường thẳng ∆1, ∆2 sao cho ∆1 ⊥ (P1), ∆2 ⊥ (P2) (Hình 31).
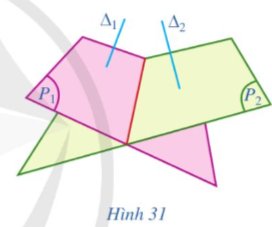
a) Nêu cách xác định góc giữa hai đường thẳng ∆1, ∆2.
b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng ∆1, ∆2 như trên hay không?
Thảo luận (1)Hướng dẫn giảia) Vẽ hai đường thẳng \(\Delta _1',\Delta _2'\) cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\).
b) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) và \(\Delta _1'\) song song (hoặc trùng) với \({\Delta _1}\) nên \(\Delta _1' \bot \left( {{P_1}} \right)\).
Tương tự ta có: \(\Delta _2' \bot \left( {{P_2}} \right)\).
Khi đó, góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\) luôn là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) nên góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) không phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 8 (SGK Cánh Diều - Tập 2 - Trang 74)
Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC'B') và (CDA'B').
Ví dụ 10. Trong không gian, cho hình lập phương ABCD.A'B'C'D'.
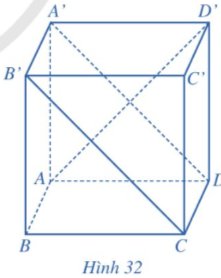
Thảo luận (1)Hướng dẫn giảiVì ADD’A’ là hình vuông nên \(AD' \bot A'D\). Vì \(CD \bot \left( {ADD'A'} \right)\) nên \(CD \bot AD'\). Do đó, \(AD' \bot \left( {CDA'B'} \right)\).
Mặt khác, \(C'D' \bot \left( {BCC'B'} \right)\), suy ra góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) là góc giữa hai đường thẳng AD’ và C’D’, đó là góc AD’C’.
Vì \(C'D' \bot \left( {ADD'A'} \right)\) nên \(C'D' \bot AD'\), suy ra . Do đó, góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) bằng 90 độ.
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 9 (SGK Cánh Diều - Tập 2 - Trang 75)
Cho hai mặt phẳng (P1) và (P2). Gọi overrightarrow{n_1}left(A_1;B_1;C_1right),overrightarrow{n_2}left(A_2;B_2;C_2right) lần lượt là hai vectơ pháp tuyến của (P1) và (P2): Δ1, Δ2 lần lượt là giá của hai vectơ overrightarrow{n_1},overrightarrow{n_2} (Hình 33). So sánh:a) cos((P1), (P2)) và cos(Δ1, Δ2);b) cos(Δ1, Δ2) và left|cosleft(overrightarrow{n_1},overrightarrow{n_2}right)right|.
Đọc tiếp
Cho hai mặt phẳng (P1) và (P2). Gọi \(\overrightarrow{n_1}=\left(A_1;B_1;C_1\right),\overrightarrow{n_2}=\left(A_2;B_2;C_2\right)\) lần lượt là hai vectơ pháp tuyến của (P1) và (P2): Δ1, Δ2 lần lượt là giá của hai vectơ \(\overrightarrow{n_1},\overrightarrow{n_2}\) (Hình 33). So sánh:
a) cos((P1), (P2)) và cos(Δ1, Δ2);
b) cos(Δ1, Δ2) và \(\left|\cos\left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|\).
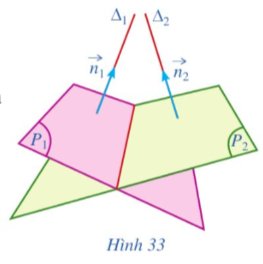
Thảo luận (1)Hướng dẫn giảia) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) nên đường thẳng \({\Delta _1}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(\left( {{P_1}} \right)\) làm một vectơ chỉ phương.
Vì \({\Delta _2} \bot \left( {{P_2}} \right)\) nên đường thẳng \({\Delta _2}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(\left( {{P_2}} \right)\) làm một vectơ chỉ phương.
Do đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai vectơ pháp tuyến \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).
Vậy \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \cos \left( {{\Delta _1},{\Delta _2}} \right)\).
b) Ta có:\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 9 (SGK Cánh Diều - Tập 2 - Trang 75)
Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow{n}=\left(A;B;C\right)\). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.
Thảo luận (1)Hướng dẫn giảiMặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\); mặt phẳng (Oxz) có một vectơ pháp tuyến là \(\overrightarrow j = \left( {0;1;0} \right)\); mặt phẳng (Oyz) có một vectơ pháp tuyến là \(\overrightarrow i = \left( {1;0;0} \right)\)
Do đó, \(\cos \left( {\left( {Oxy} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 0.B + 1.C} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);
\(\cos \left( {\left( {Oxz} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 1.B + 0.C} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| B \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);
\(\cos \left( {\left( {Oyz} \right),\left( P \right)} \right) = \frac{{\left| {1.A + 0.B + 0.C} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| A \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 1 (SGK Cánh Diều - Tập 2 - Trang 78)
Đường thẳng đi qua điểm A(3; 2; 5) nhận overrightarrow{u}left(-2;8;-7right) làm vectơ chỉ phương có phương trình tham số là:A. left{{}begin{matrix}x-2+3ty8+2tz-7+5tend{matrix}right. B. left{{}begin{matrix}x3-2ty2-8tz5-7tend{matrix}right. C. left{{}begin{matrix}x3-2ty2+8tz5+7tend{matrix}right. D. left{{}begin{matrix}x3-2ty2+8tz5-7tend{matrix}right.
Đọc tiếp
Đường thẳng đi qua điểm A(3; 2; 5) nhận \(\overrightarrow{u}=\left(-2;8;-7\right)\) làm vectơ chỉ phương có phương trình tham số là:
A. \(\left\{{}\begin{matrix}x=-2+3t\\y=8+2t\\z=-7+5t\end{matrix}\right.\) B. \(\left\{{}\begin{matrix}x=3-2t\\y=2-8t\\z=5-7t\end{matrix}\right.\) C. \(\left\{{}\begin{matrix}x=3-2t\\y=2+8t\\z=5+7t\end{matrix}\right.\) D. \(\left\{{}\begin{matrix}x=3-2t\\y=2+8t\\z=5-7t\end{matrix}\right.\)
Thảo luận (1)Hướng dẫn giảiVì thẳng đi qua điểm A(3; 2; 5) nhận \(\overrightarrow u = \left( { - 2;8; - 7} \right)\) làm vectơ chỉ phương có phương trình tham số là: \(\left\{ \begin{array}{l}x = 3 - 2t\\y = 2 + 8t\\z = 5 - 7t\end{array} \right.\) .
Chọn D
(Trả lời bởi Nguyễn Quốc Đạt)