Cho hình chóp \(S.ABC\) có \(SA = SB = SC = a,\widehat {BSA} = \widehat {CSA} = {60^ \circ },\) \(\widehat {BSC} = {90^ \circ }\). Cho \(I\) và \(J\) lần lượt là trung điểm của \(SA\) và \(BC\). Chứng minh rằng \(IJ \bot SA\) và \(IJ \bot BC\).
Bài 1. Hai đường thẳng vuông góc
Bài 3 trang 56 (SGK Chân trời sáng tạo)
Thảo luận (1)
Bài 4 trang 56 (SGK Chân trời sáng tạo)
Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thẳng \(AK\) và \(BC\).
Thảo luận (1)Hướng dẫn giảiTHAM KHẢO:
Tam giác ACD đều cạnh a có AK là trung tuyến nên AK=\(\dfrac{\sqrt{3}}{2}\)a
Gọi I là trung điểm của BD
Tam giác ABD đều cạnh a có AI là trung tuyến nên AI=\(\dfrac{\sqrt{3}}{2}\)a
Tam giác BCD có IK là đường trung bình nên IK//BC, IK=\(\dfrac{1}{2}\)BC=\(\dfrac{1}{2}\)a
Ta có: cos\(\widehat{AKI}\)=\(\dfrac{\left(\dfrac{\sqrt{3}}{2}\right)^2+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{\sqrt{3}}{2}\right)^2}{2.\dfrac{\sqrt{3}}{2}.\dfrac{1}{2}}=\dfrac{\sqrt{3}}{6}\)
Nên \(\widehat{AKI}\)=\(73,2^0\)
Vì BC//IK nên góc giữa AK và BC là góc giữa AK và KI và bằng \(73,2^0\)
(Trả lời bởi Bùi Nguyên Khải)
Giải mục 2 trang 55 (SGK Chân trời sáng tạo)
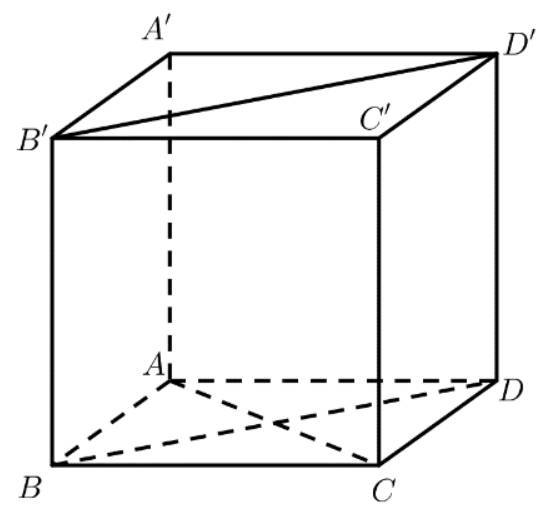
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông.
a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với \(AC\).
b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với \(AC\).
Thảo luận (1)Hướng dẫn giải
a) Các đường thẳng vuông góc với \(AC\) là: \(B{\rm{D}},B'D',AA',BB',CC',DD'\).
b) Các đường thẳng chéo với \(AC\) là: \(B'D',BB',DD'\).
(Trả lời bởi Hà Quang Minh)
Bài 2 trang 56 (SGK Chân trời sáng tạo)
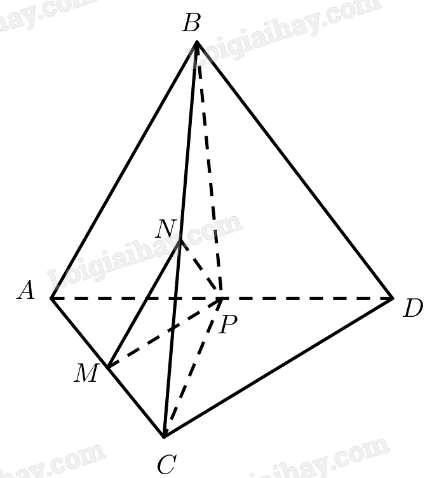
Cho tứ diện đều \(ABCD\). Chứng minh rằng \(AB \bot CD\).
Thảo luận (1)Hướng dẫn giải
Giả sử tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AC,BC,A{\rm{D}}\).
\(M\) là trung điểm của \(AC\)
\(N\) là trung điểm của \(BC\)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel AB,MN = \frac{1}{2}AB = \frac{a}{2}\)
\(M\) là trung điểm của \(AC\)
\(P\) là trung điểm của \(AD\)
\( \Rightarrow MP\) là đường trung bình của tam giác \(AC{\rm{D}}\)
\( \Rightarrow MP\parallel C{\rm{D,MP}} = \frac{1}{2}C{\rm{D}} = \frac{a}{2}\)
Ta có: \(MN\parallel AB,MP\parallel C{\rm{D}} \Rightarrow \left( {AB,C{\rm{D}}} \right) = \left( {MN,MP} \right) = \widehat {NMP}\)
Ta có: \(BP\) là trung tuyến của tam giác \(ABD\)\( \Rightarrow BP = \frac{{\sqrt {2\left( {A{B^2} + B{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(CP\) là trung tuyến của tam giác \(ACD\)\( \Rightarrow CP = \frac{{\sqrt {2\left( {A{C^2} + C{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(NP\) là trung tuyến của tam giác \(BCP\)\( \Rightarrow NP = \frac{{\sqrt {2\left( {B{P^2} + C{{\rm{P}}^2}} \right) - B{C^2}} }}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác \(MNP\) có:
\(\cos \widehat {NMP} = \frac{{M{N^2} + M{P^2} - N{P^2}}}{{2.MN.MP}} = 0 \Rightarrow \widehat {NMP} = {90^ \circ }\)
Vậy \(\left( {AB,C{\rm{D}}} \right) = {90^ \circ }\).
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 2 trang 55 (SGK Chân trời sáng tạo)
Hình bên mô tả một người thợ đang ốp gạch vào tưởng có sử dụng thước laser để kẻ vạch. Tìm các đường thẳng vuông góc với đường thẳng \(a\) trong Hình 4.

Thảo luận (1)Hướng dẫn giảiTHAM KHẢO:
Các đường thẳng vuông góc với a là: chân tường, mép các viên gạch ốp,...
(Trả lời bởi Bùi Nguyên Khải)
Giải mục 2 trang 55 (SGK Chân trời sáng tạo)
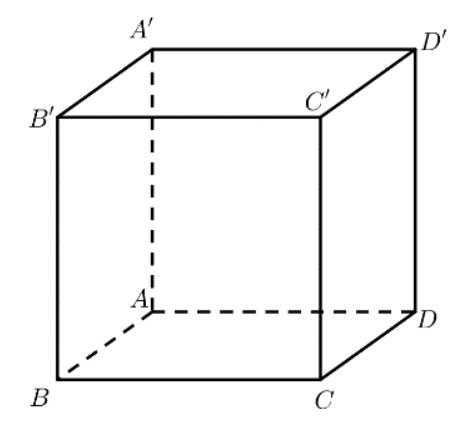
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:
a) \(AB\) và \(BB'\);
b) \(AB\) và \(DD'\).
Thảo luận (1)Hướng dẫn giải
a) \(\left( {AB,BB'} \right) = \widehat {ABB'} = {90^ \circ }\).
b) Ta có: \(DD'\parallel BB' \Rightarrow \left( {AB,DD'} \right) = \left( {AB,BB'} \right) = {90^ \circ }\).
(Trả lời bởi Hà Quang Minh)
Giải mục 1 trang 54, 55 (SGK Chân trời sáng tạo)
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA',A'D'\). Tính góc giữa các cặp đường thẳng:
a) \(MN\) và \(DD'\);
b) \(MN\) và \(CD'\);
c) \(EF\) và \(CC'\).
Thảo luận (1)Hướng dẫn giảitham khảo:
a) Trong tam giác ABC có MN là đường trung bình nên MN//AC
Mà AA' // DD'
Nên góc giữa MN và DD' là góc giữa AC Và AA'
b) Vì MN//AC nên góc giữa MN và CD' là góc giữa AC và CD'
c) Trong tam giác AA'D' có EF là đường trung bình nên EF//AD'
Mà CC'//AA'
Nên góc giữa EF và CC' là góc giữa AA' và AD'
(Trả lời bởi Bùi Nguyên Khải)
Giải mục 1 trang 54, 55 (SGK Chân trời sáng tạo)
Cho hai đường thẳng chéo nhau \(a\) và \(b\) trong không gian. Qua một điểm \(M\) tuỳ ý vẽ \(a'\parallel a\) và vẽ \(b'\parallel b\). Khi thay đổi vị trí của điểm \(M\), có nhận xét gì về góc giữa \(a'\) và \(b'\)?
Thảo luận (1)Hướng dẫn giảiKhi thay đổi vị trí của điểm $M$, góc giữa $a'$ và $b'$ sẽ không thay đổi. Điều này có nghĩa là cho dù ta di chuyển điểm $M$, hai đường thẳng $a'$ và $b'$ vẫn song song với nhau và góc giữa chúng không đổi.
(Trả lời bởi HaNa)
Giải mục 1 trang 54, 55 (SGK Chân trời sáng tạo)
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác \(OMN\) vuông cân tại \(O\). Tính góc giữa hai thanh gỗ \(a\) và \(b\).

Thảo luận (1)Hướng dẫn giảiTa có:\(a||OM\Rightarrow\left(a,b\right)=\left(OM,b\right)=\widehat{MON}=90^o\).
(Trả lời bởi Mai Trung Hải Phong)
Bài 1 trang 56 (SGK Chân trời sáng tạo)
Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).
Thảo luận (1)Hướng dẫn giảiTHAM KHẢO:
CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)
(Trả lời bởi Bùi Nguyên Khải)