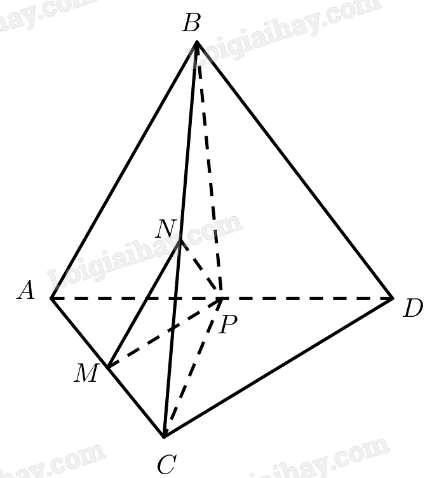
Giả sử tứ diện đều \(ABCD\) có cạnh bằng \(a\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AC,BC,A{\rm{D}}\).
\(M\) là trung điểm của \(AC\)
\(N\) là trung điểm của \(BC\)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel AB,MN = \frac{1}{2}AB = \frac{a}{2}\)
\(M\) là trung điểm của \(AC\)
\(P\) là trung điểm của \(AD\)
\( \Rightarrow MP\) là đường trung bình của tam giác \(AC{\rm{D}}\)
\( \Rightarrow MP\parallel C{\rm{D,MP}} = \frac{1}{2}C{\rm{D}} = \frac{a}{2}\)
Ta có: \(MN\parallel AB,MP\parallel C{\rm{D}} \Rightarrow \left( {AB,C{\rm{D}}} \right) = \left( {MN,MP} \right) = \widehat {NMP}\)
Ta có: \(BP\) là trung tuyến của tam giác \(ABD\)\( \Rightarrow BP = \frac{{\sqrt {2\left( {A{B^2} + B{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(CP\) là trung tuyến của tam giác \(ACD\)\( \Rightarrow CP = \frac{{\sqrt {2\left( {A{C^2} + C{{\rm{D}}^2}} \right) - A{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(NP\) là trung tuyến của tam giác \(BCP\)\( \Rightarrow NP = \frac{{\sqrt {2\left( {B{P^2} + C{{\rm{P}}^2}} \right) - B{C^2}} }}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác \(MNP\) có:
\(\cos \widehat {NMP} = \frac{{M{N^2} + M{P^2} - N{P^2}}}{{2.MN.MP}} = 0 \Rightarrow \widehat {NMP} = {90^ \circ }\)
Vậy \(\left( {AB,C{\rm{D}}} \right) = {90^ \circ }\).




