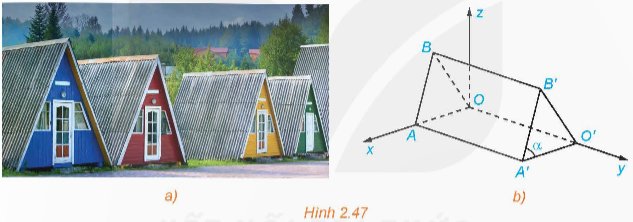
Những căn nhà gỗ trong Hình 2.47a được phác thảo dưới dạng một hình lăng trụ đứng tam giác OAB.O'A'B' như trong Hình 2.47b. Với hệ trục tọa độ Oxyz thể hiện như Hình 2.47b (đơn vị đo lấy theo centimét), hai điểm A' và B' có tọa độ lần lượt là (240; 450; 0) và (120; 450; 300). Từ những thông tin trên, có thể tính được kích thước mỗi chiều của những căn nhà gỗ không?