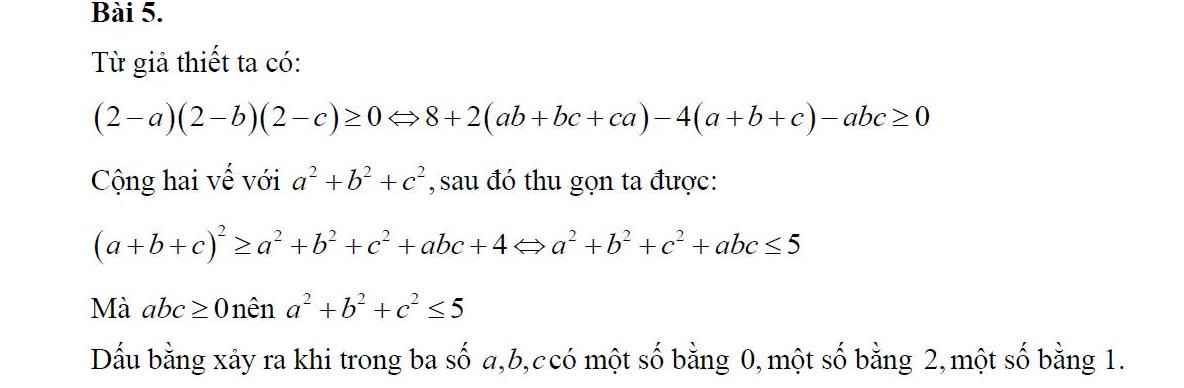Thay $x=\sqrt{\frac{1}{2,5}}; y=z=\sqrt{\frac{1}{0,25}}$ ta thấy đề sai bạn nhé!

\(VT=\dfrac{1}{\left(x-y\right)^2}+\dfrac{x^2+y^2}{x^2y^2}=\dfrac{1}{\left(x-y\right)^2}+\dfrac{\left(x-y\right)^2+2xy}{x^2y^2}\)

\(VT=\dfrac{1}{\left(x-y\right)^2}+\dfrac{\left(x-y\right)^2}{x^2y^2}+\dfrac{2}{xy}\ge2\sqrt{\dfrac{\left(x-y\right)^2}{\left(x-y\right)^2x^2y^2}}+\dfrac{2}{xy}=\dfrac{2}{\left|xy\right|}+\dfrac{2}{xy}\ge\dfrac{2}{xy}+\dfrac{2}{xy}=\dfrac{4}{xy}\)

Bài 3:

\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)

\(\Leftrightarrow x^2y^2\left(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)\ge\dfrac{4}{xy}.x^2y^2\)

\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2+y^2\ge4xy\)

\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2-2xy+y^2\ge2xy\)

\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2+\left(x-y\right)^2\ge2xy\)

\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2-2xy+\left(x-y\right)^2\ge0\)

\(\Leftrightarrow\left(\dfrac{xy}{x-y}-x+y\right)^2=0\) (luôn đúng)

-Tham khảo:

-Tham khảo:

\(VT=\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2\ge\dfrac{1}{2}\left(x+\dfrac{1}{x}+y+\dfrac{1}{y}\right)^2\)

\(VT\ge\dfrac{1}{2}\left(x+y+\dfrac{1}{x}+\dfrac{1}{y}\right)^2\ge\dfrac{1}{2}\left(x+y+\dfrac{4}{x+y}\right)^2=\dfrac{25}{2}\)

Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

Đặt \(\dfrac{x}{z}=a;\dfrac{y}{z}=b\).

Theo gt ta có \(a+b\le1\).

BĐT cần chứng minh tương đương:

\(a^2+b^2+\frac{a^2}{b^2}+\frac{b^2}{a^2}+\frac{1}{a^2}+\frac{1}{b^2}\ge \frac{21}{2}\).

Theo bđt AM - GM: \(\dfrac{a^2}{b^2}+\dfrac{b^2}{a^2}\ge2;a^2+\dfrac{1}{16}a^2\ge\dfrac{1}{2};b^2+\dfrac{1}{16}b^2\ge\dfrac{1}{2};\dfrac{15}{16}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)\ge\dfrac{15}{32}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\ge\dfrac{15}{32}.\left(\dfrac{4}{a+b}\right)^2\ge\dfrac{15}{2}\).

Cộng vế với vế của các bđt trên lại ta có đpcm.

ai lm dc bài này ko ạ. mik đang cần lắm

Giả thiết thiếu rồi em, chỗ \(\dfrac{1}{x+1}+...\) thiếu đoạn sau nữa